Persamaan garis singgung hiperbola adalah persamaan garis lurus yang melewati suatu hiperbola pada satu titik. Dengan kata lain, garis lurus dan hiperbola memiliki satu titik yang sama. Secara umum, persamaan garis lurus memiliki bentuk umum y = mx + c dengan m adalah kemiringan garis (gradien) dan c adalah konstanta.
Ada beberapa kondisi yang sering dibahas dalam pembahasan garis singgung hiperbola. Kondisi pertama adalah mencari garis singgung hiperbola jika diketahui nilai gradien m. Kondisi yang kedua adalah menentukan garis singgung hiperbola jika diketahui satu titik yang terdapat pada hiperbola. Ketiga, menentukan garis singgung hiperbola jika diketahui satu titik di luar hiperbola. Berikut ini adalah tiga kondisi garis singgung yang sering menjadi pembahasan.
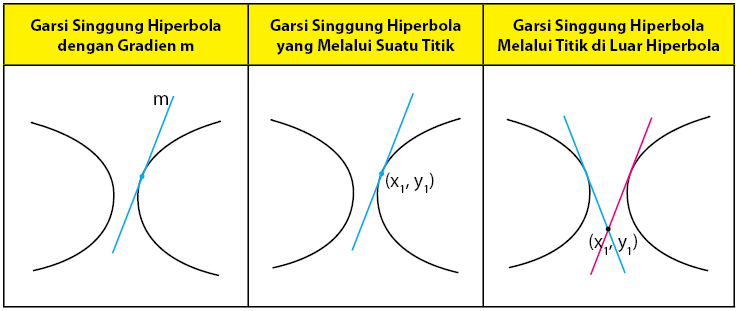
Cara menentukan garis singgung pada hiperbola tergantung pada persamaan hiperbola yang diberikan dan apa yang diketahui pada soal. Ada dua bentuk persamaan garis lurus yang menyinggung hiperbola yaitu garis lurus jika diketahui gradien m dan garis lurus jika diketahui melalui suatu titik.
Bagaimana cara menentukan garis singgung hiperbola yang diketahui memiliki nilai gradien m? Bagaimana cara menentukan garis singgung pada suatu hiperbola yang diketahui melalui sebuah titik? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Garis Singgung Hiperbola dengan Gradien m
- Garis Singgung Hiperbola yang Melalui Suatu Titik
- Contoh Soal dan Pembahasan
Garis Singgung Hiperbola dengan Gradien m
Kemiringan dari sebuah garis lurus dinyatakan dalam sebuah nilai yang disebut gradien, biasanya disimbolkan dengan huruf m. Cara menentukan garis singgung hiperbola dengan gradien m tergantung pada bentuk hiperbola yang diketahui, apakah hiperbola vertikal atau horizontal. Di mana, persamaan hiperbola memuat informasi letak pusat dan puncak hiperbola.
Perhatikan bentuk persamaan umum garis singgung yang diketahui nilai gradien m dengan suatu hiperbola pada rumus-rumus berikut.

Rumus-rumus diatas dapat digunakan untuk menentukan persamaan garis lurus yang menyinggung suatu hiperbola. Di mana terdapat keterangan berapa kemiringan atau nilai gradien dari garis lurus tersebut.
Baca Juga: Persamaan Hiperbola Hasil dari Irisan Kerucut
Garis Singgung Hiperbola yang Melalui Suatu Titik
Berikutnya, akan dibahas persamaan garis singgung pada hiperbola jika diketahui satu titik yang melalui hiperbola. Secara umum, persamaan garis singgung hiperbola yang melalui satu titik diberikan pada rumus-rumus dalam tabel di bawah.

Baca Juga: Irisan Kerucut Bentuk Hiperbola
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1: Garis Singgung yang Diketahui Melalui Satu Titik
Persamaan garis singgung hiperbola 4x2 – y2 – 40x – 4y + 48 = 0 di titik (9, 2) adalah ….
A. 4x – y – 28 = 0
B. 9x – 2y + 21 = 0
C. 4x + y – 30 = 0
D. x – y – 34 = 0
E. 9x – 2y – 34 = 0
Pembahasan:
Diketahui persamaan hiperbola 4x2 – y2 – 40x – 4y + 48 = 0 dapat dibentuk menjadi persamaan seperti berikut.
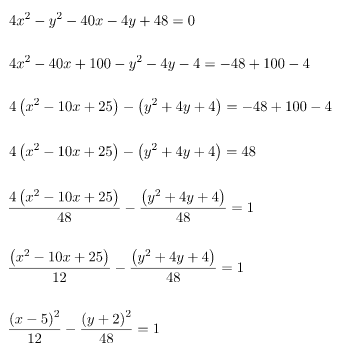
Berdasarkan persamaan hiperbola di atas, maka persamaan garis lurus yang menyinggung hiperbola menggunakan rumus berikut.
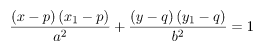
Diketahui bahwa garis singgung melalui titik (9, 2), sehingga persamaan gari lurus yang menyinggung hiperbola melalui satu titik dapat dicari seperti cara berikut.
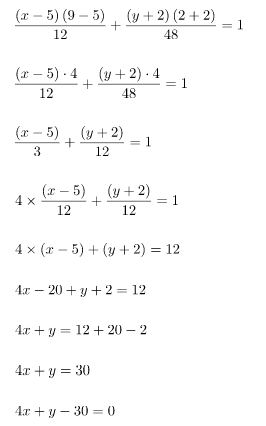
Persamaan garis singgung hiperbola 4x2 – y2 – 40x – 4y + 48 = 0 di titik (9, 2) adalah 4x + y – 30 = 0.
Jawaban: C
Baca Juga: Kedudukan Titik Terhadap Hiperbola
Contoh 2: Garis Lurus yang Menyinggung Hiperbola dan Saling Sejajar dengan Garis Lain
Persamaan garis singgung pada hiperbola dengan persamaan 4x2 – 9 y2 + 16x + 18y – 23 = 0 yang sejajar dengan garis y = 2x – 1 adalah ….
A. y = 2x + 5 + 6√2
B. y = 2x + 5 + 2√6
C. y = 2x ‒ 5 + 2√6
D. y = 2x ‒ 5 ‒ 2√6
E. y = 2x + 5 + 2√6
Pembahasan:
Persamaan garis singgung hiperbola 4x2 – 9 y2 + 16x + 18y – 23 = 0 dapat diubah menjadi persamaan seperti berikut.

Diketahui bahwa garis singgung sejajar dengan garis y = 2x – 1 maka gradiennya m = 2. Sehingga, persamaan garis singgung hiperbola dapat dicari seperti cara berikut.
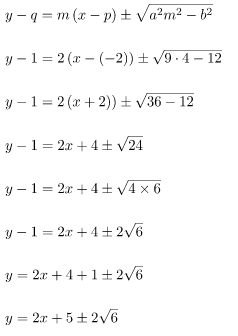
Jadi, diperoleh persamaan dua garis singgung yaitu y = 2x + 5 + 2√6 atau y = 2x + 5 ‒ 2√6.
Jawaban: B
Selesai, sekian pembahasan mengenai persamaan garis singgung hiperbola yang meliputi bentuk rumus untuk garis lurus dengan gradien m dan melalui suatu titik. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Irisan Kerucut Bentuk Parabola