Jarak bidang ke bidang pada dimensi tiga adalah jarak ruas garis terpendek yang menghubungkan kedua bidang. Ruas garis terpendek yang menjadi jarak antara dua bidang diperoleh dengan membentuk sebuah bidang baru yang memotong kedua bidang secara tegak lurus. Perpotongan bidang baru yang dibuat dengan kedua bidang berupa dua garis. Jarak antara dua garis tersebut merupakan jarak bidang ke bidang.
Rumus untuk mencari jarak bidang ke bidang dapat menggunakan Teorema Pythagoras, fungsi trigonometeri, aturan cosinus, luas segitiga, atau rumus lain yang berkaitan. Penggunaa rumus bergantung dari informasi apa yang dimiliki.
Cara menghitung jarak bidang ke bidang bisa dicari tahu dengan lebih dari satu cara. Meski demikian, pemilihan cara yang tepat akan mempermudah proses perhitungan yang dilakukan.
Bagaimana cara menghitung jarak bidang ke bidang? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Menentukan Jarak Bidang ke Bidang
Sebelum melakukan perhitungan jarak bidang ke bidang, sobat idschool perlu menentukan mana segmen garis atau ruas garis terpendek yang menghubungkan kedua bidang tersebut. Caranya dilakukan dengan bantuan bidang baru yang tegak lurus dengan kedua bidang tersebut, misalkan bidang α.
Perpotongan bidang α dengan kedua bidang berupa sebuah garis lurus. Jarak kedua garis yang menjadi perpotongan antara bidang tersebut merupakan jarak bidang ke bidang.

Jarak kedua garis tersebut dapat ditentukan dengan langkah penyelesaian berikut.
- Ambil sembarang titik pada salah satu garis
- Proyeksikan titik pada satu garis lainnya
- Hubungkan titik pada satu garis dengan hasil proyeksi titik pada garis lainnya sehingga terbentuk sebuah segmen garis
- Panjang segmen garis yang diperoleh sama dengan jarak titik ke bidang
Cara Menghitung Jarak Bidang ke Bidang
Bagaimana cara menghitung jarak bidang ke bidang diawali dengan menentukan segmen garis yang menjadi jarak anara ke dua bidang. Selanjutnya baru dilakukan perhitungan panjang segmen garis tersebut.
Untuk melihat bagaimana cara menghitung jarak bidang ke bidang, perhatikan langkah penyelesaian soal berikut.
Soal:
Balok ABCD.EFGH mempunyai panjang 4 cm, lebar 2 cm, dan tinggi 3 cm. Tentukan jarak antara bidang ABCD dan EFGH!
Jawab:
Bidang yang tegak lurus dengan bidang ABCD dan EFGH adalah ADHE (atau BCGF). Garis perpotongan antara bidang ADHE dengan bidang ABCD adalah AD. Garis perpotongan antara bidang ADHE dan bidang EFGH adalah EH.
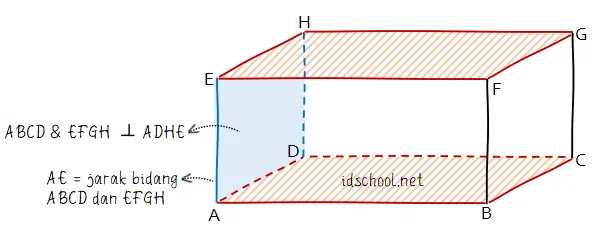
Dengan demikian jarak bidang ABCD ke bidang EFGH sama dengan jarak garis AD ke garis EG. Jarak garis AD ke garis EH pada balok ABCD.EFGH sama dengan tinggi balok.
Sehingga, jarak bidang ABCD ke EFGH = jarak garis AD ke EH = tinggi balok = 3 cm. Jadi, jarak jarak antara bidang ABCD dan EFGH adalah 3 cm.
Baca Juga: Kumpulan Rumus dan Materi Dimensi Tiga
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idshcool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal jarak bidang ke bidang
Jarak bidang ACH dan bidang EGB pada kubus ABCD.EFGH dengan rusuk 6√3 cm adalah …..
A. 4√3 cm
B. 2√3 cm
C. 4 cm
D. 6 cm
E. 12 cm
Pembahasan:
Bidang yang tegak lurus dengan bidang ACH dan EGB adalah bidang BDHF.

Garis HP adalah segmen garis perpotongan antara bidang BDHF dan ACH. Garis BQ adalah ruas garis perpotongan antara bidang BDHF dan EGB.
Jarak bidang ACH dan EGB sama dengan jarak antara garis HP dan BQ. Jarak titik HP ke BQ sama dengan ruas garis PR. Di mana titik R adalah titik hasil proyeksi titik P pada garis BQ.
Perhatikan segitiga BPQ! Di mana segitiga tersebut dapat dipandang dengan dua cara. Pertama adalah segitiga dengan alas = PB dan tinggi = PQ. Kedua adalah segitiga dengan alas = BQ dan tinggi = PR.
Diketahui panjang rusuk kubus = 6√3 dan titik P adalah titik perpotongan diagonal bidang pada kubus. Sehingga panjang PB = 1/2 × panjang diagonal bidang = 1/2×6√3×√2 = 3√6 cm. Sementara panjang ruas garis PQ = rusuk kubus = 6√3 cm.
Untuk panjang BQ dapat dihitung dengan Teorem Pythagoras dari segitiga PBQ yaitu BQ2 = BP2 + PQ2 = (3√6)2 + (6√3)2 = 54 + 108 = 162. Sehingga panjang BQ = √162 = √(81×2) = √81 × √2 = 9√2 cm.
Diketahui panjang PB = 3√6 cm; PQ = 6√3 cm; dan BQ = 9√2 cm. Ketiga panjang ruas garis tersebut dapat digunakan untuk menghitung panjang ruas garis PR seperti berikut.
Menghitung panjang garis PR:
LΔBPQ = LΔBPQ 1/2 × BQ × PR = 1/2 × PB × PQ
9√2 × PR = 3√6 × 6√3 9√2 × PR = 18√(6×3)
√2 × PR = 2√18
Menyederhanakan bentuk akar nilai PR: kalikan dengan akar sekawan penyebut
PR = √36 = 6 cm
Jadi, jarak bidang ACG dan bidang EGB adalah PR = 6 cm.
Jawaban: D
Baca Juga: Jarak Titik ke Garis pada Dimensi Tiga
Contoh 2- Soal jarak bidang ke bidang
Diketahui panjang sebuah rusuk kubus adalah 8 cm. Titik P, titik Q, titik R, dan titik S berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan HG. Jarak bidang FPQ ke bidang DRS adalah ….
A. 16 cm
B. 14 cm
C. 12 cm
D. 10 cm
E. 8 cm
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh gambar seperti berikut.
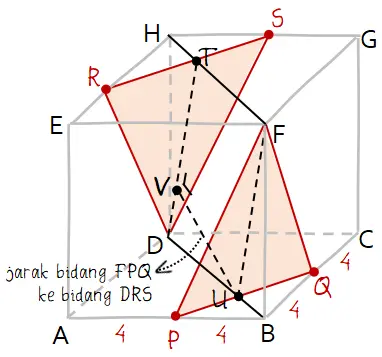
Bidang yang tegak lurus dengan bidang FPQ dan DRS adalah bidang BDHF. Bidang tersebut memotong kedua bidang masing-masing pada ruas garis DT dan FU.
Jarak bidang FPQ ke bidang DRS sama dengan jarak garis DT ke garis FU. Untuk proyeksi titik U pada garis DT adalah titik V, jarak garis DT ke garis VU sama dengan panjang ruas garis UV.
Panjang garis UV dapat dihitung dari persamaan luas jajar genjang BDTF. Namun sebelumnya perlu menghitung panjang garis FU = TD dan garis DU =TF terlebih dahulu.
Segittiga PBQ adalah segitiga siku-siku sama kaki, sehingga panjang garis PQ = 4√2 cm. Dengan cara yang sama dapat diperoleh panjang garis RS = 4√2 cm (pada segitiga RHS).
Garis BD adalah garis diagonal bidang kubus dengan panjang rusuk 8 cm. Dengan begitu, panjang garis BD = FH = rusuk√2 = 8√2 cm.
Perhatikan segitiga PBQ dan RSH! Dari kedua segitiga tersebut dapat dihitung panjang BU dan HT seperti langkah perhitungan berikut.
1a) Menghitung panjang BU:
LΔPBQ = LΔPBQ
1/2×PQ×BU = 1/2×PB×BQ 4√2 × BU = 4 × 4
BU = 4/√2 × √2/√2
BU = 4√2/2 = 2√2 cm
1b) Menghitung panjang HT:
LΔRHS = LΔRHS
1/2×RS×HT = 1/2×HR×HS 4√2 × HT = 4 × 4
BU = 4/√2 × √2/√2
BU = 4√2/2 = 2√2 cm
Diperoleh panjang BU = HT = 2√2 cm, sehingga panjang DU = TF = 8√2 – 2√2 = 6√2 cm. Panjang BU dapat digunakan untuk menghitung panjang FU dan panjang HT dapat digunakan untuk menghitung panjang TD.
2) Menghitung panjang FU: perhatikan segitiga FBU
FU2 = BU2 + FB2 = (2√2)2 + 82
FU2 = 8 + 64 = 72
FU = √72 = √(36×2)
FU = √36 × √2 = 6√2 cm
Panjang garis TD dapat dihitung dengan cara yang sama saat menghitung FU, TD = FU = 6√2 cm. Selanjutnya perhatikan jajar genjang DUFT pada kubus seperti gambar berikut.
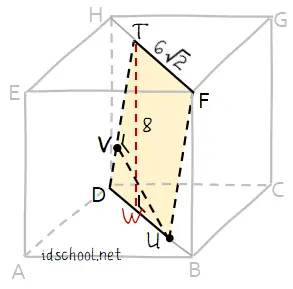
Proyeksi titik T pada garis DU adalah titik W sehingga TW = tinggi jajar genjang = panjang rusuk kubus = 8 cm.
Jajar genjang DUFT dapat dipandang dengan dua cara. Pertama adalah jajar genjang dengan alas DU dan tinggi WT. Kedua adalah jajar genjang dengan alas TD dan tinggi UV.
Mencari panjang UV:
L DUFT = L DUFT
TD × UV = DU × TW 6√2 × UV = 6√2 × 8
UV = 8 cm
Jadi jarak bidang FPQ ke bidang DRS sama dengan UV = 8 cm.
Jawaban: E
Demikianlah tadi ulasan jarak bidang ke bidang. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Rumus2 nya detail dan penjelasan nya juga detail jadinya memuaskan
Dalam rumus2 matematika ini sangat detail dan penjelasan nya juga detail jadi memuaskan juga