Gerak parabola digambarkan dengan lintasan melengkung, menyerupai setengah lingkaran. Sumbu y mewakili gerak lurus berubah beraturan (GLBB), sedangkan sumbu x mewakili gerak lurus beraturan (GLB). Persamaan-persamaan dalam gerak parabola dirangkum dalam rumus gerak parabola. Contoh lintasan gerak parabola pada kehidupan sehari-hari dapat dilihat pada bola yang dilambungkan ke atas, lintasan yang dilalui peluru dari senapan, dan lain sebagainya.
Sebelum mengetahui detail uraian lintasan gerak parabola, sebaiknya sobat idschool mengetahui bagaimana gambaran umum gerak parabola terlebih dahulu. Lintasan gerak parabola membentuk kurva mulus, bentuknya kurang lebih menyerupai grafik parabola pada persamaan kuadrat. Perhatikan ilustrasi gerak parabola dapat dilihat pada lintasan yang dilalui bom dari letukan meriam.
Bahasan pada rumus gerak parabola meliputi kecepatan pada arah vertikal Vy, kecepatan pada arah mendatar Vx, jarak maksimum, tinggi maksimum, waktu untuk mencapai ketinggian maksimum, waktu untuk mencapai jarak maksimum, dan lain sebagainya. Bagaimanakah persamaan yang belaku pada rumus gerak parabola? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Definisi Gerak Parabola
Gerak parabola atau yang biasa disebut dengan gerak peluru dapat dikatakan sebagai gabungan antara gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB). Seperti yang sudah disinggung sebelumnya bahwa sumbu x mewakili gerak GLB dan sumbu y mewakili gerak GLBB.
Lintasan yang dilalui pada gerak parabola termasuk dalam bidang dua dimensi. Gerak parabola dari suatu benda membentuk sudut elevasi dengan sumbu x atau sumbu y. Walaupun terdiri dari dua komposisi gerak, namun kedua gerak ini tidak saling memengaruhi.
Gambar lintasan gerak parabola dan keterangannya dapat dilihat seperti berikut.
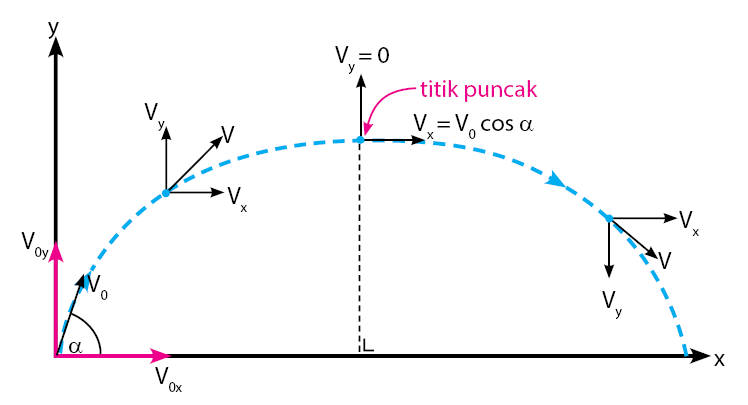
Dari gambar di atas dapat terlihat jelas bahwa terdapat kombinasi komponen penyusun gerak parabola. Komponen tersebut adalah ketinggaian, jarak horizontal, kecepatan vertikal, kecepatan horizontal, dan lain sebagainya.
Baca Juga: Pengantar GLB dan GLBB
Rumus Gerak Parabola
Pembahasan sebelumnya telah diberkan penjabaran komponen penyusun gerak parabola yang dinyatakan melalui vektor-vektor. Selain penjabaran komponen, pembahasan gerak parabola juga meliputi rumus gerak parabola. Rumus-rumus tersebut meliputi berapa jarak maksimal yang dapat ditempuh, berapa ketinggian yang dapat dicapai, berapa waktu yang dibutuhkan untuk mencapai titik tertinggi, berapa waktu yang dibutuhkan untuk mencapai jarak maksimal, dan masih banyak lagi.
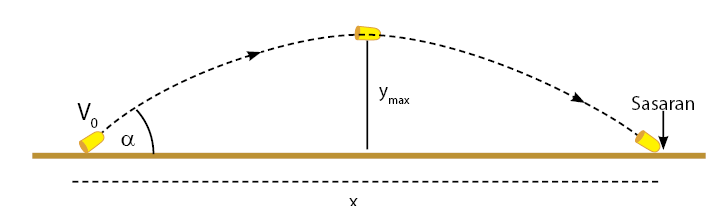
Gambar di bawah menunjukkan arah gerak parabola dan rumus gerak parabola.

Beberapa ringkasan rumus gerak parabola yang tersusun atas komponen arak vertikal (sumbu y) dan komponen arah horizontal (sumbu x) dapat dilihat pada tabel di bawah.

Untuk menambah pemahaman sobat idschool akan diberikan contoh soal gerak parabola dan cara menggunakan rumus gerak parabola yang telah diberikan di atas.
Perhatikan gambar berikut ini!
Sebuah peluru ditembakkan dengan kelajuan awal 100 m/s dan sudut elevasi 37o. Jika percepatan gravitasi bumi 10 m/s2, sin 37o = 0.6, dan cos 37o = 0.8 maka tentukan unsur – unsur berikut.
Kecepatan awal terhadap arah horizontal (sumbu x):
V0x = V0 ⋅ cos α
V0x = 100 × 0.8
V0x = 80 m/s
Kecepatan awal terhadap arah vertikal (sumbu y):
V0y = V0 ⋅ sin α
V0y = 100 × 0.6
V0y = 60 m/s
Waktu yang diperlukan peluru untuk mencapai titik tertinggi:

Kecepatan peluru saat mencapai titik tertinggi:
- Arah vertikal: Vy = 0
- Arah Horizontal
Vx = V0 ⋅ cos α
Vx = 100 ⋅ 0,8 = 80 m/s
Tinggi maksimum yang bisa dicapai peluru (ymax):

Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar):
Waktu untuk mencapai jarak mendatar paling jauh adalah dua kali waktu untuk mencapai ketinggian maksimum, yaitu 2 × 6 = 12 sekon.
Jarak terjauh yang dicapai peluru (xmax):
Dapat diperoleh menggunakan rumus: xmax = V0t ⋅ cos α. karena sudah sudah diketahui waktu untuk mencapai jarak maksimum, yaitu 12 sekon.
Menghitung jarak terjauh yang dapat ditempuh:
xmax = V0t ⋅ Cos α
xmax = 100 × 12 × 0.8
xmax = 960 meter
Baca Juga: Kumpulan Rumus pada Gerak Melingkar Beraturan
Contoh Soal dan Pembahasan
Soal – soal berikut dapat sobat idschool gunakan untuk menambah pemahaman sobat idschool terkait bagaimana cara menggunakan rumus gerak parabola. Setiap soal telah disertai pembahasan yang dapat sobat idschool gunakan sebagai acuan pengerjaan.
Contoh 1 – Soal Gerak Parabola
Perhatikan gambar di bawah!

Sebuah bola dilontarkan dari atap sebuah gedung yang tingginya adalah h = 10 m dengan kelajuan awal V0 = 10 m/s. Jika percepatan gravitasi bumi adalah 10 m/s2, sudut yang terbentuk antara arah lemparan bola dengan arah horizontal adalah 30o (gesekan bola dengan udara diabaikan). Waktu yang diperlukan bola untuk menyentuh tanah dan jarak mendatar yang dicapai bola berturut-turut adalah ….
A. 2 dan 10√3
B. 1 dan 10√3
C. 2 dan 5√3
D. 1 dan 5√3
E. 2 dan 7√3
Pembahasan:
Mencari waktu yang diperlukan bola untuk menyentuh tanah ketinggian gedung h atau sama dengan y.
y = V0t ⋅ sin α – ½gt2
y = 10 ⋅ t ⋅ sin 30o – ½ ⋅ 10 ⋅ t2
–10 = 10 ⋅ ½ ⋅ t – ½ ⋅ 10 ⋅ t2
–10 = 5t – 5t2
5t2 – 5t + 10 = 0
t2 – t + 2 = 0
(t – 2)(t + 1) = 0
t = 2 atau t = –1
Sehingga waktu yang diperlukan bola untuk menyentuh tanah dari ketinggian h = 10 dari atas gedung adalah 2 sekon (ambil nilai positif).
Mencari jarak mendatar yang dicapai bola:
x = V0t ⋅ cos α
x = 10 ⋅ 2 ⋅ cos 30o
x = 10 ⋅ 2 ⋅ ½√3
x = 10√3 meter
Jadi, waktu yang diperlukan bola untuk menyentuh tanah adalah 2 sekon dan jarak yang dapat dicapai bola dalah 10√3 meter.
Jawaban: A
Baca Juga: Titik Berat Benda 2 Dimensi
Contoh 2 – Penggunaan Rumus Gerak Parabola
Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30o. Ketinggian maksimum yang dicapai adalah ….
A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
Pembahasan:
Berdasarkan soal, dapat diperoleh informasi seperti berikut.
Kecepatan awal: V0 = 60 m/s
Besar sudut elevasi: α= 30o
Baca Juga: Gaya Gesek
Sehingga, ketinggian maksimum dapat dicari seperti pada cara penyelesaian berikut.
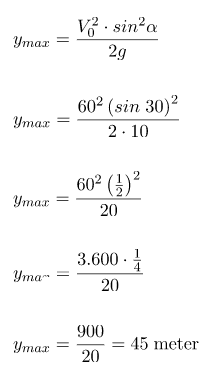
Jawaban: B
Contoh 3 – Penggunaan Rumus Gerak Parabola
Peluru ditembakkan condong ke atas dengan kecepatan awal 1,4 × 103 m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 × 105 m. Bila percepatan gravitasi 9,8 m/s2, maka besar sudut elevasinya adalah ….
A. 10o
B. 30o
C. 45o
D. 60o
E. 75o
Baca Juga: Aturan Penulisan Angka Penting
Pembahasan:
Berdasarkan informasi pada soal dapat diperoleh informasi bahwa.
> Kecepatan mula-mula: V0= 1,4 × 103 m/s
> Jarak terjauh: xmax = 2 × 105 m
Besar sudut elevasi dapat diperoleh dari rumus jarak mendatar maksimum, caranya adalah sebagai berikut.
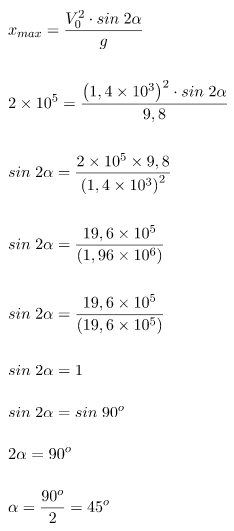
Jawaban: C
Contoh 4 – Penggunaan Rumus Gerak Parabola
Perhatikan gambar berikut!
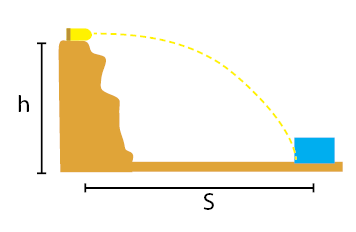
Sebuah peluru ditembakkan dari moncong sebuah meriam dengan kelajuan 50 m/s arah mendatar dari atas sebuah bukit. Jika percepatan gravitasi bumi adalah 10 m/s2 dan ketinggian bukit 100 m. Waktu yang diperlukan peluru untuk mencapai tanah dan jarak mendatar yang dicapai peluru (S) adalah ….
A. 2√5 dan 50√5
B. 2√5 dan 100√5
C. 5√5 dan 50√5
D. 5√5 dan 100√5
E. 7√5 dan 50√5
Pembahasan:
Waktu yang diperlukan peluru untuk mencapai tanah dapat diperoleh menggunakan rumus ketinggian y.
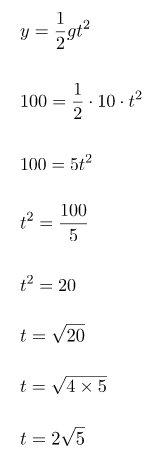
Jarak mendatar yang dicapai peluru dapat diperoleh dari jarak mendatar yang merupakan gerakan berupa GLB dengan besar sudut terhadap horizontal sama dengan nol. Sehingga, untuk menghitung jarak yang dapat dicapai peluru dapat menggunakan rumus jarak secara langsung.
S = V × t
S = 50 × 2√5
S = 100√5 meter
Jawaban: B
Sekian pembahasan rumus gerak parabola yang dilengkapi dengan keterangan arah gerak, definisi, dan contoh penggunaan rumus gerak parabola untuk menyelesaikan soal. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Besaran Pokok dan Besaran Turunan