Rumus perkalian fungsi sinus dan cosinus adalah fungsi identitas yang memuat perkalian fungsi sinus atau fungsi cosinus. Bentuk perkalian dapat berupa perkalian antara fungsi sinus, perkalian antara fungsi cosinus, atau perkalian antara fungsi sinus dengan cosinus. Rumus perkalian fungsi sinus dan cosinus dapat digunakan untuk membantu menentukan nilai fungsi trigonometri (khusunya dengan besar sudut tidak istimewa) tanpa alat bantu hitung.
Rumus perkalian fungsi sinus dan cosinus memiliki hubungan identitas dengan rumus jumlah/selisih fungsi sinus atau rumus jumlah/selilsih fungsi cosinus. Ada empat rumus perkalian fungsi sinus dan cosinus yang terdiri dari persamaan-persamaan di bawah.

Baca Juga: Rumus Trigonometri Sudut Rangkap
Bagaimana cara mendapat identitas rumus perkalian fungsi sinus dan cosinus? Bagaimana cara penggunaan rumus perkalian fungsi sinus dan cosinus? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Rumus Sin α × Sin β
Penjabaran rumus perkalian fungsi sinus dan cosinus yang pertama akan dibahas adalah perkalian dua sudut sinus dengan besar sudut berbeda. Ada cara yang dapat digunakan untuk menghafal rumus perkalian dua fungsi sinus dengan besar sudut berbeda. Cara tersebut adalah menghafal rumus perkalian dua sudut sinus menggunakan kalimat: min dua sin sin sama dengan cos jumlah dikurang cos selisih
Bentuk rumus perkalian fungsi sin dikali sin dengan besar sudut α dan sudut β adalah sebagai berikut.
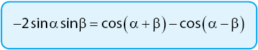
Bukti:
Pembuktian rumus perkalian fungsi sinus dan cosinus dapat menggunakan rumus-rumus jumlah dan selisih dua sudut pada fungsi trigonometri. Jika belum tahu atau belum hafal bisa lihat dulu di sini.
Selanjutnya perhatikan pengurangan antara rumus jumlah dan selisih dua sudut fungsi sinus.
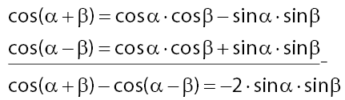
Hasil pengurangan pada dua persamaan di atas sama dengan ‒2 × sin α × sin β = cos(α + β) ‒ cos(α ‒ β).
[Terbukti]
Selanjutnya akan ditunjukkan penggunaan rumus perkalian sinus pada contoh soal dan pembahasan penggunaan salah satu bentuk rumus perkalian fungsi sinus dan cosinus berikut.
Contoh soal:
Diketahui besar sudut α = 75o dan sudut β = 15o. Maka nilai sin α × sin β adalah .…
A. 3/4
B. 1/2
C. 1/4
D. ‒1/4
E. ‒3/4
Pembahasan:
‒2 × sin α × sin β = cos (α + β) ‒ cos (α ‒ β)
‒2 × sin α × sin β = cos ( 75o + 15o) ‒ cos ( 75o ‒ 15o)
‒2 × sin α × sin β = cos 90o ‒ cos 60o
‒2 × sin α × sin β = 0 ‒ 1/2
‒2 × sin α × sin β = ‒1/2
sin α × sin β = ‒1/2 : ‒2
sin α × sin β = ‒1/2 × (‒1/2 ) = 1/4
Jawaban: C
Rumus Cos α × Sin β
Rumus perkalian fungsi sinus dan cosinus yang kedua adalah rumus perkalian anatra fungsi cosinus dengan fungsi sinus. Untuk menghafal rumus perkalian cos dan sin dapat menggunakan kalimat pernyataan: dua cos sin sama dengan sin jumlah dikurang sin selisih.
Bentuk rumus perkalian fungsi cos dan fungsi sin dengan besar sudut α dan sudut β adalah sebagai berikut.
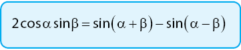
Bukti:
Pembuktian rumus cos di kali sin dapat menggunakan rumus penjumlahan dan selisih dua sudut pada fungsi sinus. Perhatikan cara di bawah.

Hasil pengurangan pada dua persamaan di atas sama dengan: 2 × cos α × sin β = sin (α + β) + sin (α ‒ β)
[Terbukti]
Contoh soal:
Diketahui besar sudut α = 75o dan sudut β = 15o, maka nilai cos α × sin β adalah .…
A. ¼(2 + √3)
B. ¼(2 ‒√3)
C. ¼(3 ‒ √2)
D. ¼(3 + √3)
E. ¼(3 ‒ √3)
Pembahasan:
2 × cos α × sin β = sin (α + β) ‒ sin (α ‒ β)
2 × cos α × sin β = sin (75o + 15o) ‒ sin (75o ‒ 15o)
2 × cos α × sin β = sin 90o ‒ sin 60o
2 × cos α × sin β = 1 ‒ 1/2√3
2 × cos α × sin β = 1/2(2 ‒ 1/2√3)
cos α × sin β = 1/2(2 ‒ 1/2√3) : 2
cos α × sin β = 1/2(2 ‒ 1/2√3) × 1/2
cos α × sin β = 1/4(2 ‒ 1/2√3)
Jawaban: B
Baca Juga: Penjumlahan dan Pengurangan Fungsi Sin dan Cos
Rumus Sin α × Cos β
Rumus perkalian sinus dan cosinus yang akan dipelajari lebih lanjut adalah rumus sin dikali cos. Cara untuk menghafal perkalian sin dikali cos dapat menggunakan kalimat: dua sin cos sama dengan sin jumlah ditambah sin selisih. Bentuk rumus perkalian fungsi sin dan cos dengan besar sudut α dan sudut β sesuai dengan persamaan berikut.

Bukti:
Pembuktian rumus sin dikali cos dapat menggunakan pengurangan rumus jumlah dan selisih dua sudut fungsi sinus. Langkahnya dapat dilihat pada gambar berikut.

Hasil penjumlahan pada dua persamaan di atas sama dengan: 2 × sin α × cos β = sin (α + β) + sin (α ‒ β)
[Terbukti]
Contoh Soal:
Diketahui besar sudut α = 75o dan sudut β = 15o, Maka nilai sin α × cos β adalah .…
A. 1/4(2 + √3)
B. 1/4(2 ‒ √3)
C. 1/4(3 ‒ √2)
D. 1/4(3 + √3)
E. 1/4(3 ‒ √3)
Pembahasan:
2 × sin α × cos β = sin (α + β) + sin (α ‒ β)
2 × sin α × cos β = sin (75o + 15o) + sin (75o ‒ 15o)
2 × sin α × cos β = sin 90o + sin 60o
2 × sin α × cos β = 1 + 1/2√3
2 × sin α × cos β = 1/2(2 + 1/2√3)
sin α × cos β = 1/2(2 + 1/2√3) : 2
sin α × cos β = 1/2(2 + 1/2√3) × 1/2
sin α × cos β = 1/4(2 + 1/2√3)
Jawaban: A
Rumus Cos α × Cos β
Selanjutnya adalah rumus cos dikali cos. Kalimat yang dapat digunakan untuk menghafal rumus cos dikali cos adalah dua cos cos sama dengan cos jumlah ditambah cos selisih. Rumus perkalian fungsi cos dengan besar sudut α dan fungsi cos dengan besar sudut β sesuai dengan persamaan berikut.

Bukti:
Bukti rumus cos dikali cos dapat menggunakan pengurangan rumus jumlah dan selisih dua sudut fungsi cosinus. Selanjutnya perhatikan cara di bawah,

Hasil penjumlahan pada dua persamaan di atas sama dengan: 2 × cos α × cos β = cos (α + β) + cos (α ‒ β)
[Terbukti]
Contoh Soal:
Diketahui besar sudut α = 75o dan sudut β = 15o, maka nilai cos α × cos β adalah ….
A. 3/4
B. 1/2
C. 1/3
D. 1/4
E. 1/5
Pembahasan:
2 × cos α × cos β = cos (α + β) + cos (α ‒ β)
2 × cos α × cos β = cos (75o + 15o) + cos (75o ‒ 15o)
2 × cos α × cos β = cos 90o + cos 60o
2 × cos α × cos β = 0 + 1/2
cos α × cos β = 1/2 : 2
cos α × cos β = 1/2 × 1/2 = 1/4
Jawaban: D
Demikianlah ulasan tentang rumus perkalian fungsi sinus dan cosinus. Terimakasih sudah mengunjungi idschool(dot)net. Semoga bermanfaat!
Baca Juga: Kumpulan Rumus Transformasi Geometri (Translasi, Refleksi, Rotasi, dan Dilatasi)