Transpose matriks A disimbolkan dengan AT adalah matriks yang diperoleh dengan cara menukar elemen pada baris menjedi elemen pada kolom. Dengan demikian, pada bukan matriks persegi, jumlah kolom dan baris ikut berubah. Kondisi ini tentu akan membuat matriks awal dan matriks hasil transpose memiliki ukuran yang berbeda.
Contoh matriks dan transpose secara umum dinyatakan seperti berikut.
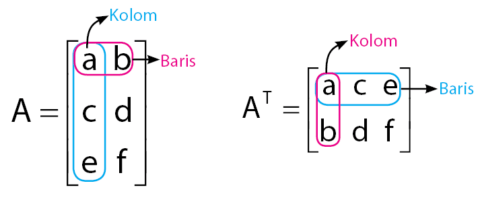
Sifat-sifat matriks transpose:
1. (A + B)T = AT + BT
2. (AT)T = A
3. (k × A)T = k × AT
4. (AB)T = BT · AT
Baca Juga: Determinan dan Invers Matriks (+sifat-sifatnnya)
Contoh soal cara menentukan transpose suatu matriks:
Misalkan diketahui sebuah matriks A dengan ukuran 3 x 2:
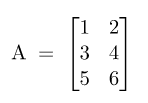
Maka transpose matriks A adalah:
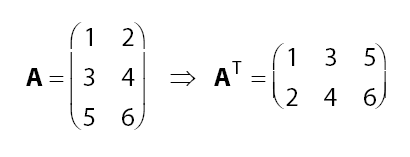
Sekian pembahasan mengenai matriks transpose, semoga bermanfaat!
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks
damerenita9@gmail.com