Selain bangun ruang sisi datar, dalam pembahasan bangun ruang juga terdapat bangun ruang sisi lengkung. Perbedaan antara bangun ruang sisi datar dan bangun ruang sisi lengkung terletak pada bentuk sisi yang menyusunnya. Pada bangun ruang sisi datar, semua sisinya lurus dan tidak ada yang melengkung. Sedangkan pada bangun ruang sisi lengkung memiliki sisi yang melengkung.
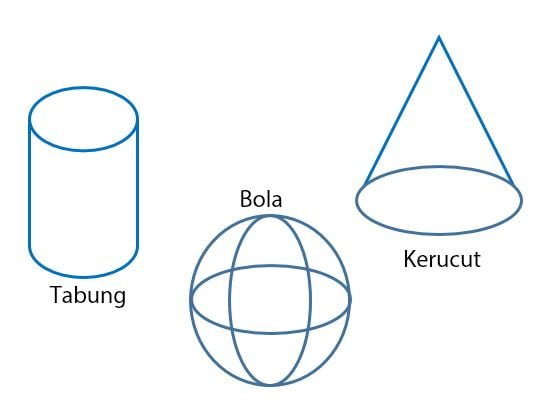
Bangun ruang merupakan dimensi tiga. Artinya, benda tersebut mempunyai ruang yang bisa ditempati. Sisi lengkung dicirikan dengan permukaan yang tidak datar. Contoh bangun ruang sisi lengkung adalah tabung, kerucut, dan bola.
Baca Juga: Bangun Ruang Sisi Datar
Dalam bahasan bangun ruang sisi lengkung biasa dipelajari bagaimana cara mencari isi/volume suatu bangun dan luas permukaan dari suatu bangun ruang sisi lengkung. Bagaimana caranya? Simak ulasan lebih lengkapnya pada masing – masing bahasan berikut.
Table of Contents
Tabung
Bangun ruang sisi lengkung pertama yang diulas adalah tabung. Bentuk tabung dengan bagian lengkap meliputi dua buah lingkaran sebagai alas tabung dan tutup tabung. Serta bagian selimut tabung yang menghubungkan bagian alas dan tutup tabung. Berikut ini adalah keterangan bagian-bagian tabung.
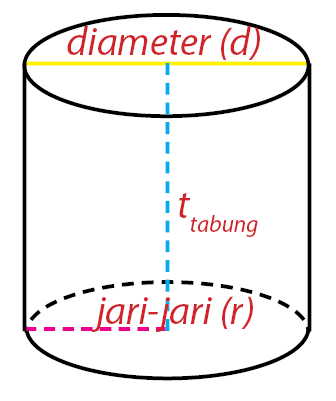
Karakteristik Tabung:
i) Mempunyai 3 bidang sisi, yaitu bidang alas, bidang tutup, dan sisi tegak.
ii) Sisi tegak pada tabung merupakan bidang lengkung atau disebut selimut tabung.
iii) Tabung mempunyai dua rusuk.
iv) Tinggi tabung adalah jarak antara titik pusat lingkaran alas dengan titik pusat lingkaran tutup.
Jaring-Jaring Tabung:
Seperti yang telah disebutkan sebelumnya bahwa tabung terdiri atas bagian alas/tutup tabung yang berbentuk lingkaran dan selimut tabung. Gambar jaring-jaring tabung dapat dilihat seperti berikut.
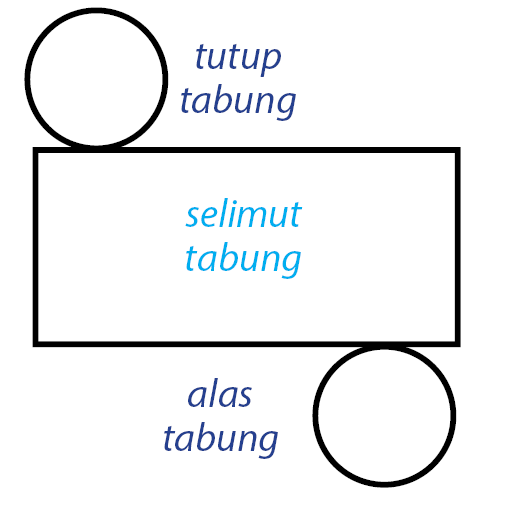
Rumus Luas Permukaan dan Volume Tabung
Rumus pada tabung yang akan diberikan di bawah merupakan rumus tabung yang dapat digunakan untuk menghitung luas permukaan tabung, luas permukaan tabung tanpa tutup, dan juga rumus volume tabung.
Luas alas/tutup tabung = Luas Lingkaran
Lalas = π × r2
Ltutup = π × r2
Luas selimut tabung: Ls. tabung = 2×π×r×t
Luas permukaan tabung:
Lp. tabung = 2 × Lalas + Ls. tabung
Lp. tabung = 2 × π × r2 + 2 π × r × t
Lp. tabung = 2×π×r(r + t)
Luas permukaan tabung tanpa tutup:
Lp. tabung = Lalas + Ls. tabung
Lp. tabung = π×r2 + 2π×r×t
Lp. tabung = πr(r + 2t)
Volume tabung:
Vtabung = Lalas × t
Vtabung = π×r2×t
Baca Juga: Rumus Volume dan Luas Permukaan Balok
Kerucut
Kedua adalah jenis bangun ruang sisi lengkung berupa kerucut. Kerucut merupakan limas dengan alasnya berbentuk lingkaran. Gambar kerucut dapat dilihat seperti gambar di bawah.
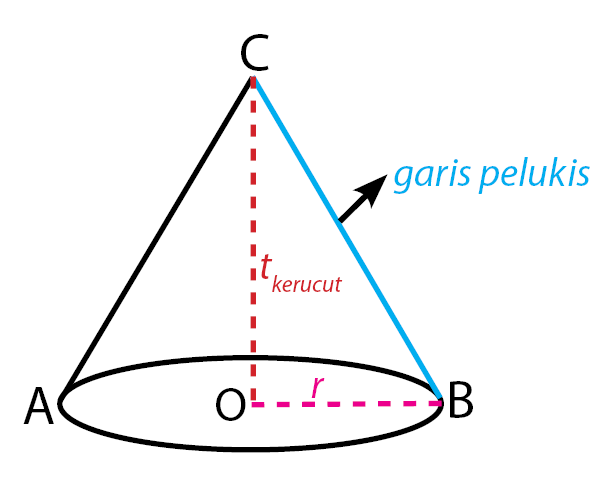
Karakteristik Kerucut:
i) Mempunyai 2 bidang sisi, yaitu bidang alas (lingkaran) dan bidang lengkung (selimut kerucut).
ii) Memiliki 1 (satu) buah rusuk.
iii) Memiliki 1 (satu) buah titik sudut.
Jaring-Jaring Kerucut:
Jaring-jaring kerucut terdiri atas bagian lingkaran dan sebuah lingkaran. Secara lebih jelasnya dapat dilihat pada gambar jaring-jaring kerucut di bawah.

Rumus Luas Permukaan dan Volume Kerucut
Bahasan rumus pada kerucut yang diberikan adalah rumus untuk mencari garis pelukis, rumus luas permukaan kerucut, dan rumus volume kerucut.
Panjang garis pelukis: s = √(r2 + t2)
Luas selimut kerucut: Ls. kerucut = π×r×s
Luas permukaan kerucut:
Lp. tabung = Lalas + Ls. Kerucut
Lp.tabung = π×r2 + π×r2×s
Lp.tabung = π×r×(r + s)
Volume Kerucut:
Vkerucut = 1/3 × Lalas × t
Vkerucut = 1/3 ×π× r2×t
Baca Juga: Cara Menghitung Volume Gabungan dari 2 atau Lebih Bangun Ruang
Bola
Selanjutnya adalah bangun ruang sisi lengkung yang ketiga yaitu Bola. Bola digambarkan seperti gambar di bawah.

Karakteristik Bola:
i) Bola adalah bangun ruang yang dibatasi oleh sebuah bidang sisi yang berbentuk lengkung.
ii) Bola tidak mempunyai rusuk dan tidak mempunyai titik sudut.
Rumus Luas Permukaan dan Volume Bola:
Rumus pada bola meliputi rumus untuk menghitung luas permukaan bola, luas permukaan setengah bola, luas permukaan setengah bola padat, dan rumus volume bola. Berikut ini adalah kumpulan beberapa rumus pada bola
Luas seluruh permukaan bola:
L p. bola = 4×π×r2
Luas permukaan setengah bola:
Lp. ½bola = 2 ×π×r2
Luas permukaan setengah bola padat:
Lp. bola padat = 3×π×r2
Volume bola: Vbola = 4/3 ×π×r3
Baca Juga: Cara Menghitung Volume dan Luas Permukaan 1/2 Bola Padat
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Bangun Ruang Sisi Lengkung
Sebuah kerucut mempunyai jari-jari alas dengan panjang 5 cm dan panjang garis pelukis 13 cm. Tinggi kerucut tersebut adalah .…
A. 7 cm
B. 8 cm
C. 10 cm
D. 12 cm
Pembahasan:
Berdasarkan soal dapat diketahui bahwa:
- Jari-jari kerucut = r = 5 cm
- Garis pelukis kerucut = s = 13 cm
Perhatikan ΔTOP dalam kerucut seperti gambar di bawah.
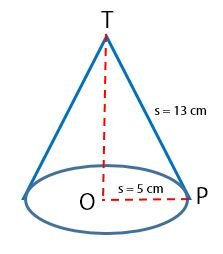
Untuk mencari tinggi kerucut dapat menggunakan teorema phytagoras seperti yang ditunjukkan pada cara berikut.
t2 = s2 − r2
t2 =132 − 52
t2 = 169 − 25
t2 = 144 → t = √144 = 12 cm
Jadi, tinggi kerucut tersebut adalah 12 cm.
Jawaban: D
Baca Juga: Kesebangunan dan Kekongruenan
Contoh 2 – Soal Bangun Ruang Sisi Lengkung
Perhatikan gambar di bawah!

Jika luas permukaan bola 90 cm2, maka luas seluruh permukaan tabung adalah ….
A. 160 cm2
B. 150 cm2
C. 135 cm2
D. 120 cm2
Pembahasan:
Persamaan pada Bola:
Lp. bola = 4×π×r2
90 = 4×π×r2
2×π×r2 = 90/2 = 45 cm2
Persamaan pada Tabung:
Jari-jari tabung = jari-jari bola = r
Tinggi tabung = 2 x jari-jari bola = 2r
Sehingga,
Lp. tabung = 2×π×r2 + 2×π×r×t
Lp. tabung = 2×π×r2 + 2×π×r×2r
Lp. tabung = 2×π×r2 + 2×(2×π×r2)
Lp. tabung = 3×45 = 135 cm2
Proses perhitungan sudah selesai, namun di sini, idschool akan menambahkan cara cepat untuk menyelesaikan contoh soal seperti di atas. Simak langkah – langkahnya seperti berikut ini.
CARA CEPAT!!!
Jika bola di dalam tabung menyinggung alas dan tutup tabung maka rbola = rtabung. Luas permukaan tabung dapat dihitung seperti cara di bawah.
Ltabung = 3/2 × Lbola
Ltabung = 3/2 × 90 = 135 cm2
Jadi, luas seluruh permukaan tabung adalah 135 cm2.
Jawaban : C
Contoh 3 – Soal Bangun Ruang Sisi Lengkung
Sebuah kerucut mempunyai volume 27 cm3. Jika diameter kerucut diperbesar 3 kali dan tingginya diperbesar 2 kali, maka volume kerucut tersebut adalah .…
A. 972 cm3
B. 486 cm3
C. 324 cm3
D. 162 cm3
Pembahasan:
Misalkan jari-jari kerucut pertama adalah r1 dan tinggi kerucut pertama adalah r1 maka memenuhi persamaan di bawah.
Vkerucut = 27
1/3 ×π×r12×t1 = 27
Berdasarkan keterangan pada soal diameter kerucut diperbesar 3 kali, sehingga dapat dibentuk persamaan berikut.
d2 = 3 × d1
2r2 = 3 × 2r1
r2 = 32r1
Berdasarkan pada soal tingginya diperbesar 2 kali: t2 = 21
Sehingga, volume kerucut dengan diameter kerucut diperbesar 3 kali dan tingginya diperbesar 2 kali dapat dihitung seperti cara berikut.
V2 = 1/3×π×r22×t2
V2 = 1/3×π×(3r1)2×2t1
V2 = 1/3×π×9r12×2t
V2 = 18×(1/3×π×r12×t1)
V2 = 18×27 = 486 cm3
Jawaban: B
Demikianlah ulasan terkait materi bangun ruang sisi lengkung yang meliputi tabung, kerucut, dan bola. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Rumus Kesebangunan Trapesium