Rumus panjang garis singgung lingkaran adalah d2 = J2 − (R ± r)2 di mana d = panjang garis singgung lingkaran luar/dalam. Sementara J = jarak kedua pusat lingkaran, R = panjang jari-jari lingkaran besar, dan r = panjang jari-jari lingkaran kecil.
Garis singgung lingkaran persekutuan dua lingkaran terdiri dari dua macam yaitu garis singgung luar lingkaran dan garis singgung dalam lingkaran. Antara garis singgung lingkaran luar/dalam dengan jarak kedua pusat lingkaran dan jumlah/selisih jari-jari lingkaran dapat membentuk segitiga siku-siku.
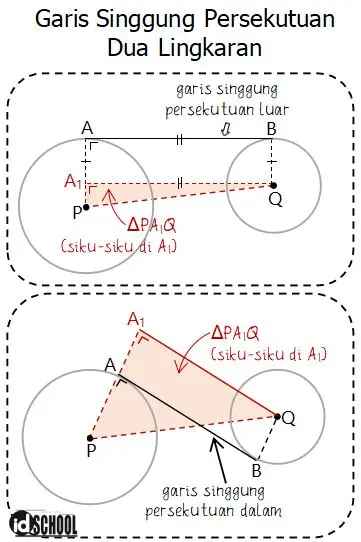
Sehingga, cara mencari panjang garis singgung lingkaran luar/dalam dapat menggunakan Rumus Pythagoras.
Bagaimana cara menghitung panjang garis singgung lingkaran luar? Bagaimana cara menghitung panjang garis singgung lingkaran dalam pada persekutuan dua lingkaran? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar Isi:
Baca Juga: Unsur-Unsur Lingkaran dan Rumus Keliling & Luasnya
Panjang Garis Singgung Lingkaran Luar
Dua buah lingkaran yang berpusat pada titik O dan P memiliki panjang jari-jari yang berbeda. Sebuah garis menyinggung kedua lingkaran pada titik A dan titik B.
Diketahui bahwa panjang jari-jari lingkaran dengan pusat O adalah R, sedangkan panjang jari-jari lingkaran dengan pusat P adalah r.
Selain itu diketahui pula jarak kedua pusat pada dua lingkaran tersebut sama dengan OP. Panjang garis singgung lingakaran luar persekutuan 2 lingkaran sama dengan panjang ruas garis AB pada gambar di bawah.

Keterangan:
AB = garis singgung luar lingkaran
OP = jarak kedua pusat lingkaran
R = jari-jari lingkaran O
r = jari-jari lingkaran P
Panjang garis singgung lingkaran luar pada persekutuan dua lingkaran sama dengan panjang ruas garis AB. Di mana panjang ruas garis AB sama dengan panjang ruas gari PP’.
Perhatikan segitiga siku-siku PP’O dengan sudut siku-siku di P’. Sehingga ketiga sisi pada segitiga siku-siku tersebut membentuk persamaan P’P2 = OP2 ‒ P’O2.
Diketahui bahwa P’O = OA ‒ BP = R ‒ r dan panjang P’P = AB. Sehingga dapat diperoleh rumus panjang garis singgung lingkaran luar yaitu AB2 = OP2 ‒ (R ‒ r)2.

Baca Juga: Rumus Luas Juring dan Panjang Busur Lingkaran
Panjang Garis Singgung Lingkaran Dalam
Cara menghitung panjang garis singgung lingkaran dalam pada persekutuan dua lingkaran tidak jauh berbeda dengan garis singgung lingkaran luar. Keduanya dapat sama-sama dihitung menggunakan rumus Pythagoras. Bedanya hanya terletak pada posisi garis singgung lingkaran.
Dua titik singgung pada garis singgung lingkaran luar terletak di sisi yang sama. Sedangkan pada garis singggung persekutuan dalam memiliki dua titik singgung pada dua sisi bersebrangan.
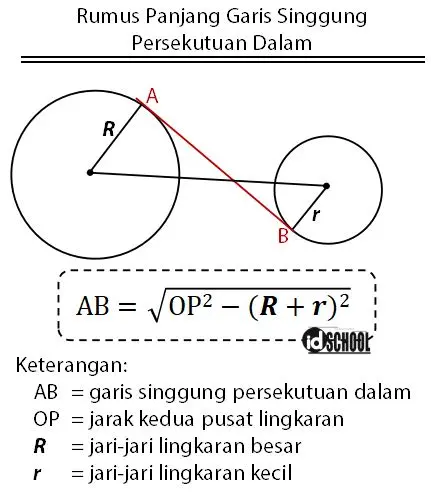
Bentuk garis singgung lingkaran dalam terdapat pada gambar berikut.

Keterangan:
AB = garis singgung dalam lingkaran
OP = jarak kedua pusat lingkaran
R = jari-jari lingkaran O
r = jari-jari lingkaran P
Saat garis singgung AB digeser sejauh jari-jari lingkaran kecil sehingga melewati pusat lingkaran P maka akan membentuk segitiga PP’O. Sehingga didapat segitiga siku-siku dengan ketiga sisinya yaitu P’O, P’P, dan OP.
Sebuah segitiga siku-siku memenuhi rumus Pythagoras. Untuk segitiga PP’O memenuhi persamaan P’P2 = OP2‒ P’O2.
Diketahui bahwa PO’ = OA + BP = R + r dan panjang P’P = AB maka diperoleh rumus panjang garis singgung lingkaran dalam yaitu AB2 = OP2‒ (R + r)2.
Baca Juga: Sudut Pusat dan Sudut Keliling Lingkaran
Contoh Soal Garis Singgung Persekutuan Dua Lingkaran dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap soal di bawah juga terdapat pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Garis Singgung Lingkaran Luar
Dua buah lingkaran memiliki panjang garis singgung persekutuan luar 24 cm dan jarak kedua titik pusat lingkaran 26 cm.
Jika panjang jari-jari lingkaran besar 18 cm, maka panjang jari-jari lingkaran yang lain adalah ….
A. 6 cm
B. 8 cm
C. 9 cm
D. 10 cm
Pembahasan:
Berdasarkan data pada soal, kita dapat peroleh gambar di bawah.
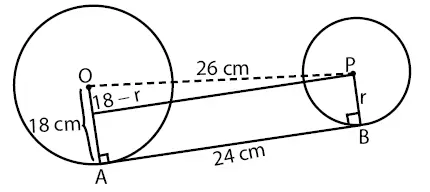
Diketahui nilai panjang garis singgung, jarak kedua pusat, dan panjang jar-jari kedua lingkaran seperti berikut.
- Panjang garis singgung lingkaran luar: AB = 24 cm
- Jarak kedua pusat lingkaran: OP = 26 cm
- Panjang jari-jari lingkaran besar: OA = 18 cm
- Panjang jari-jari lingkaran kecil: OB = r
Menghitung panjang jari-jari lingkaran yang belum diketahui (OB):
AB2 = OP2 ‒ (OA ‒ r)2
242 = 262 ‒ (18 ‒ r)2
676 = 576 ‒ (18 ‒ r)2
(18 ‒ r)2 = 676 ‒ 576 = 100
18 ‒ r = √100 =10
‒r = 10 ‒ 18 = ‒8
r = 8 cm
Jadi, panjang jari-jari lingkaran yang lain adalah r = 8 cm.
Jawaban: D
Contoh 2 – Soal Garis Singgung Lingkaran Dalam Persekutuan Dua Lingkaran
Perhatikan gambar berikut!

Panjang jari-jari lingkaran besar dan kecil berturut-turut adalah 10 cm dan 5 cm. Jarak kedua pusat lingkaran adalah 25 cm.
Panjang garis singgung AB adalah ….
A. 12 cm
B. 15 cm
C. 17 cm
D. 20 cm
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh informasi berikut.
- Jari-jari lingkaran besar: R = 10 cm
- Jari-jari lingkaran kecil: r = 5 cm
- Jarak pusat 2 lingkaran: OP = 25 cm
Menghutng panjang garis singgung lingkaran dalam (AB):
AB2 = OP2 ‒ (R + r )2
AB2 = 252 ‒ ( 10 + 5)2
AB2 = 625 ‒ 225 = 400
AB = √400 = 20 cm
Jadi, panjang garis singgung lingkaran dalam adalah AB = 20 cm.
Jawaban: D
Sekian pembahasan mengenai panjang garis singgung lingkaran luar dan dalam pada persekutuan dua lingkaran. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Segitiga Siku-Siku dengan Sudut Istimewa (α = 30o, 45o, atau 60o)
ayo sini by1 beatbox
Sangat membantu🙏🏿😋
Sangat menarik dan mudah dipahami
Kalian jangan sembarangan yaa jangan lupa MESIN YANG KOREKSI!!
Cukup dipahami
Boong Bu
Jangan lupa nonton di yt ARSGaming ya gess yaaa
Sulit dipahami semoga harimu Senin terus
bukan saya itu bu, zhaky arya yang ngetik
Terima kasih 🙏
Ini sangat membantu dalam kegiatan belajar saya selama di rumah. 🙏😊😊
Hali Umi, terimakasih juga atas komentar dan kunjungannya!