Hubungan Antar Dua Garis dan Sudut yang Terbentuk

Hubungan Antar Dua Garis dan Sudut Yang Terbentuk merupakan materi yang mengulas hubungan antar dua garis yang berpotongan serta sudut yang terbentuk dari perpotongan dua garis sejajar oleh sebuah garis. Hubungan dua garis dapat berupa berpotongan, sejajar, berimpit, dan bersilangan. Sedangkan sudut yang terbentuk dari perpotongan dua garis sejajar oleh sebuah garis dapat berupa sudut sehadap, bertolak belakang, dalam bersebrangan, luar bersebrangan, sepihak, dan luar sepihak.

Sudut yang terbentuk dari perpotongan dua garis dapat memungkinkan menghitung besar sudut lain jika diketahui besar suatu sudut. Misalkan diketahui besar sebuah sudut dari sudut yang terbentuk pada perpotongan dua garis sejajar oleh sebuah garis. Informasi besar sudut yang diberikan tersebut dapat memungkinkan untuk menghitung besar sudut lain. Bagaimana caranya? sobat idschool dapat mencari tahu cara mengetahui besar sudut dalam hubungan antar sudut melalui ulasan pada halaman ini.

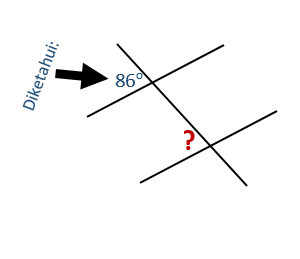
Baca juga: Persamaan Garis Lurus

Materi hubungan antara dua garis dan sudut yang terbentuk sering keluar di ujian nasional. Jadi, sebaiknya sobat idschool menyimak dengan baik materi mengenai hubungan antar dua garis dan sudut yang terbentuk berikut.

Table of Contents

• Hubungan Antar Dua Garis
• Jenis Sudut dan Besar Sudut yang Terbentuk dari Perpotongan Dua Garis
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Besar Sudut Berpelurus
  • Contoh 2 – Soal Besar Sudut

Hubungan Antar Dua Garis

Garis adalah kumpulan titik-titik yang banyaknya tak terhingga yang saling bersebelahan dan memanjang ke kedua arah. Hubungan antara dua garis dapat berupa sejajar, berpotongan, berimpit, dan bersilangan.

Berimpit
Dua garis tersebut dikatakan berimpit jika semua titik pada sebuah garis terletak pada garis lainnya, atau sebaliknya.

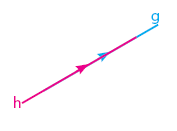
Dua Garis Sejajar:
Karakteristik dua garis sejajar adalah kedua garis terletak pada satu bidang datar dan tidak mempunyai titik persekutuan (titik potong).

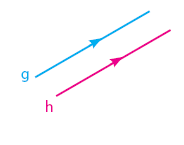
Berpotongan:
Dua garis dikatakan berpotongan jika dua garis itu mempunyai satu titik persekutuan (titik potong).

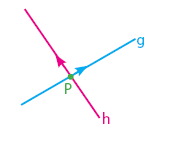
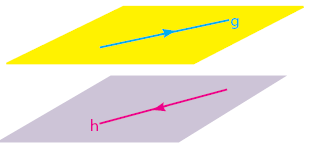
Dua Garis Bersilangan:
Dua garis bersilangan jika kedua garis terletak pada bidang yang berbeda dan kedua garis tidak sejajar dan tidak berpotongan.

Baca Juga: Cara Menentukan Sudut Antara Dua Tali Busur Lingkaran yang Berpotongan

Jenis Sudut dan Besar Sudut yang Terbentuk dari Perpotongan Dua Garis

Sebelum melanjutkan materi mengenai hubungan antar dua garis dan sudut yang terbentuk, mari kita mengenal sudut terlebih dahulu. Sudut adalah daerah yang dibatasi oleh dua sinar garis yang bertemu di satu titik pangkal. Perhatikan gambar sudut di bawah.

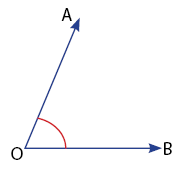
Keterangan: O = titik pangkal, OA dan OB = kaki sudut, dan ∠AOB = daerah sudut.

Dilihat dari besar sudutnya, jenis – jenis sudut meliputi sudut lancip, sudut siku – siku, sudut tumpul, sudut lurus, dan sudut refleks. Kriteria masing – masing jenis sudut dapat disimak pada penjelasan di bawah.

Jenis – Jenis Sudut:

1. Sudut Lancip: 0^o ≤ θ < 90^o

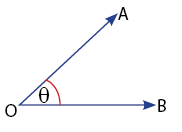
2. Sudut Siku-Siku θ = 90^o

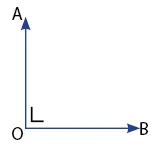
3. Sudut Tumpul: 90^o < θ < 180^o

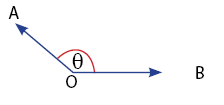
4. Sudut Lurus θ ≤ 180^o

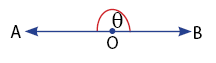
5. Sudut Refleks 180^o < θ < 360^o

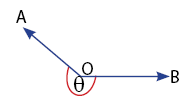
Pembahasan hubungan antar sudut juga memuat hubungan sudut komplemen dan suplemen. Apa itu sudut komplemen dan sudut suplemen? Simak penjelasannya berikut.

Komplemen ~ Sudut Berpenyiku

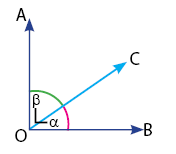
Hubungan antar sudut komplemenL:
Penyiku ∠α = ∠β
Penyiku ∠β = ∠α
Jumlah besar ∠α + ∠β = 90^o

Sudut Berpelurus (Suplemen)

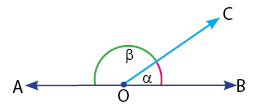
Hubungan antar sudut suplemen:
Pelurus ∠α = ∠β
Pelurus ∠β = ∠α
Jumlah besar ∠α + ∠β = 180^o

Sudut-Sudut yang Terbentuk Oleh Dua Garis Sejajar dan Dipotong Sebuah Garis

Dua buah garis sejajar, yaitu garis g dan garis h, dipotong oleh sebuah garis yang tidak sejajar dengan keduanya. Dari perpotongan garis tersebut akan terbentuk sudut – sudut yang terdiri atas sudut sehadap, bertolak belakang, dalam bersebrangan, luar bersebrangan, sepihak, dan luar sepihak.

Perhatikan gambar di bawah!

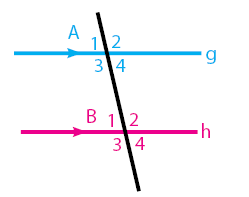
Pasangan sudut-sudut sehadap: memiliki besar sudut yang sama
∠A₁ = ∠B₁
∠A₂ = ∠B₂
∠A₃ = ∠B₃
∠A₄ = ∠B₄

Sudut dalam berseberangan: mempunyai besar sudut yang sama
∠A₄ = ∠B₁
∠A₃ = ∠B₂

Sudut luar berseberangan: mempunyai besar sudut yang sama
∠A₁ = ∠B₄
∠A₂ = ∠B₃

Pasangan sudut saling bertolak belakang: mempunyai besar sudut yang sama
∠A₁ = ∠A₄
∠A₂ = ∠A₃
∠B₁ = ∠B₄
∠B₂ = ∠B₃

Pasangan sudut dalam sepihak: jumlah sudutnya adalah 180^o
∠A₃ +∠B₁ = 180^o
∠A₄ + ∠B₂ = 180^o

Sudut Luar Sepihak: jumlah sudutnya 180^o
∠A₁ + ∠B₃ = 180^o
∠A₂ + ∠B₄ = 180^o

Baca Juga: Sudut Pusat dan Sudut Keliling pada Lingkaran

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan hubungan antar dua garis dan sudut di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Besar Sudut Berpelurus

Perhatikan gambar berikut!

Besar pelurus sudut KLN adalah ….
A. 31^o
B. 72^o
C. 85^o
D. 155^o

Pembahasan:

Jumlah dua sudut yang saling berpelurus adalah 180o, maka dapat diperoleh persamaan dan penyelesaian untuk mencari nilai x seperti berikut.

Mencari nilai x:
(3x + 15)^o + (2x + 10)^o = 180^o
5x + 25^o = 180^o
5x = 180^o ‒ 25^o
5x = 155^o
x = ¹⁵⁵/₅ =31^o

Besar pelurus ∠KLN = besar ∠MLN:
m ∠MLN = 2x + 10^o
m ∠KLN = 2×31^o + 10^o
m ∠KLN = 62^o + 10^o = 72^o

Jadi, besar pelurus sudut KLN adalah 72^o.

Jawaban: B

Contoh 2 – Soal Besar Sudut

Perhatikan gambar berikut!

Besar ∠BAC adalah ….
A. 78^o
B. 76^o
C. 55^o
D. 50^o

Pembahasan:
Untuk menyelesaikan jenis soal ini, sobat idschool dapat melakukan dua cara yang berbeda dengan hasil yang sama. Simak kedua cara menyelesaikan soal besar sudut seperti di atas dan pilih cara terbaik yang sobat idschool sukai.

Cara 1:

Menghitung besar ∠ACB:
∠ACB + ∠BCD = 180^o
∠ACB + 114^o = 180^o
∠ACB = 180^o – 114^o = 66^o

Selanjutnya hitung nilai x melalui ΔACB, perhatikan ΔABC dan INGAT bahwa jumlah ketiga sudut pada segitiga adalah 180^o.

∠BAC + ∠ABC + ∠ACB = 180^o
x + (x + 4^o) + 66^o = 180^o
2x + 70^o = 180^o
2x = 180^o – 70^o
2x = 110^o
x = ¹¹⁰/₂ = 55^o

Jadi, besar ∠BAC = x = 55^o

Cara 2: mencari nilai x dengan cara kedua dapat dikatakan sebagai rumus cepat.

Mencari nilai x:
x + (x + 4^o) = 114^o
2x = 114^o – 4^o
2x = 110^o
x = ¹¹⁰/₂ = 55^o

Jadi, besar ∠BAC = x = 55^o

Jawaban: C

Oke, sekian materi mengenai hubungan antar dua garis dan sudut yang terbentuk, mudah bukan? Jika sobat idschool memiliki pertanyaan mengenai hubungan antar dua garis dan sudut yang terbentuk bisa tanyakan lewat komentar. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Aritmatika Sosial – SMP