Perhatikan gambar berikut!
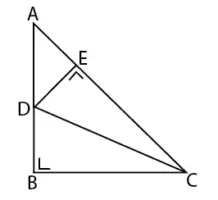
Segitiga ABC adalah segitiga siku-siku sama kaki. Jika AB = 10 cm dan CD garis bagi sudut C maka panjang BD adalah . . . .
A. 5 cm
B. (10√2 − 10) cm
C. (10 − 5√2) cm
D. (5√2 − 5) cm
Pembahasan:
Diketahui bahwa segitiga ABC adalah segitiga sama kaki dan panjang AB = 10 cm, sehingga panjang BC = AB = 10 cm. Dari soal juga memberikan keterangan bahwa garis CD adalah garis bagi sudut BCA, sehingga besar ∠BCD = ∠ECD.
Panjang sisi yang menghadap besar sudut yang sama adalah sama panjang, sehingga panjang sisi BD = DE. Segitiga ADE adalah segitiga sama kaki karena siku-siku di E dan besar ∠DAE = 45o sehingga besar ∠AED = 45o.
Gambaran segitiga beserta ukurannya sesuai informasi yang diberikan pada soal terdapat pada gambar di bawah.
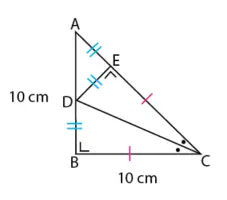
Segitiga ABC adalah segitiga siku-siku di titik B sehingga besar ∠ABC = 90o. Segitiga ABC juga merupakan segitiga sama kaki sehingga besar ∠BCA = ∠BCA = 45o.
Diketahui AB = 10 cm dan CD garis bagi sudut C maka panjang BD dapat diketahui dengan menghitung panjang AE. Di mana panjang BD = AE = AC − CE, dengan panjang CE = 10 cm dan panjang AC belum diketahui.
Panjang sisi AC dapat diketahui dengan rumus pada Teorema Pythagoras. Cara menghitung panjang AC dilakukan seperti cara berikut.
Menghitung panjang AC:
AC2 = AB2 + BC2
AC2 = 102 + 102
AC2 = 100 + 100 = 200
AC = √200 = 10√2 cm
Menghitung panjang BD:
BD = DE = AE
BD = AC − CE
BD = 10√2 cm − 10 cm
BD = (10√2 − 10) cm
Jadi, jika AB = 10 cm dan CD garis bagi sudut C maka panjang BD adalah (10 √2 − 10) cm.
Jawaban: B