Definit Negatif dan Definit Positif Fungsi Kuadrat, Apa Itu?
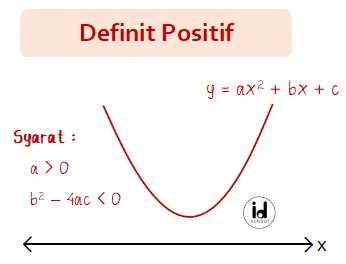
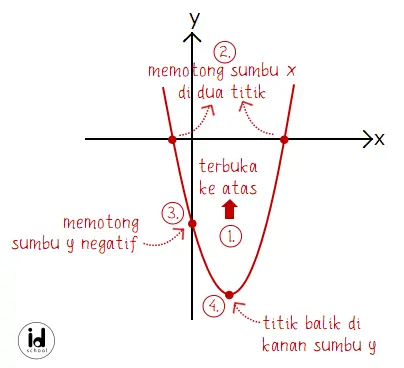
Definit positif fungsi kuadrat adalah suatu kondisi di mana fungsi kuadrat akan selalu bernilai positif. Sedangkan definit negatif adalah suatu kondisi di mana fungsi kuadrat akan selalu memiliki nilai negatif. Dalam bentuk kurva, definit positif fungsi kuadrat nampak pada bentuk parabola yang terbuka ke atas dan terletak di atas sumbu x. Untuk definit negatif memiliki […]
Definit Negatif dan Definit Positif Fungsi Kuadrat, Apa Itu? Read More »