Dalam suatu lingkaran berjari-jari 10 cm terdapat segi-8 beraturan.

Dalam suatu lingkaran berjari-jari 10 cm terdapat segi-8 beraturan. Panjang sisi segi-8 tersebut adalah ….
A. 10√(2 ‒ √2) cm
B. 10√(2 ‒ 2√2) cm
C. 10√(2 + 2√3) cm
D. 5√(2 ‒ √2) cm
E. 5√(2 + √2) cm

Jawab: A

Berikut ini adalah ilustrasi gambar untuk segi delapan beraturan di dalam lingkaran dengan panjang jari-jari sama dengan 10 cm.

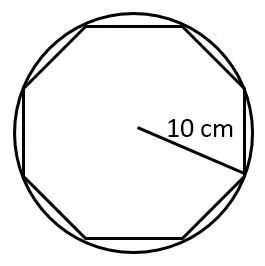
Untuk mencari panjang sisi segi delapan, kita perlu mengetahui besar sudut puncak segitiga pada segi delapan = ^360o/₈ = 45⁰. Seperti terlihat pada gambar di bawah.

Panjang sisi segi delapan sama dengan panjang AB. Cara menghitung panjang AB dapat dilakukan dengan rumus aturan cosinus.

Menghitung panjang AB:
AB² = OA² + OB² ‒ 2×OA×OB×cos 45^o
AB² = 10² + 10² ‒ 2×10×10×½√2
AB² = 100 + 100 ‒ 100√2 = 200 ‒ 100√2
AB = √(200 ‒ 100√2) = √100(2 ‒ √2)
AB = √100 × √(2 ‒ √2) = 10√(2 ‒ √2) cm