Diketahui segitiga PQR dengan P(0, 1, 4), Q(2, -3, 2), dan R (-1, 0, 2). Besar sudut PQR adalah …

Diketahui segitiga PQR dengan P(0 1 4), Q(2, -3, 2), dan R (-1, 0, 2). Besar sudut PQR adalah ….
A. 120^o
B. 90^o
C. 60^o
D. 45^o
E. 30^o

Jawab: E

Segitiga PQR pada soal dapat diilustrasikan seperti berikut.

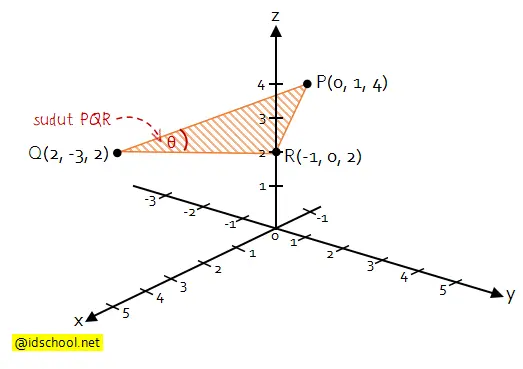
Besar sudut PQR sama dengan besar sudut antara ruas garis QP dan QR. Nilai besar sudut dapat dicari menggunakan aturan cosiunus.

PR² = PQ² + RQ² ‒ 2·PQ·RQ·cos θ

Di mana PR, PQ, dan RQ adalah panjang tiga sisi segitiga PQR. Sementara θ adalah sudut antara dua sisi segitiga.

Diketahui titik koordinat P, Q, dan R. Panjang sisi segitiga PQR sama dengan jarak antara dua titik koordinat pada segitiga PQR.

Rumus jarak dua titik (x₁, y₁, z₁) dan (x₂, y₂, z₂):

d = √[(x₁ ‒ x₂)² + (y₁ ‒ y₂)² + (z₁ ‒ z₂)²]

Diketahui titik koordinat:
P(0, 1, 4)
Q(2, ‒3, 2)
R(‒1, 0, 2)

Panjang PR:
|PR| = √[(0‒(‒1))² + (1 ‒ 0)² + (4 ‒ 2)²]
|PR| = √[1² + 1² + 2²]
|PR| = √[1+1+4] = √6

Panjang PQ:
|PQ| = √[(0‒2)² + (1‒(‒3))² + (4‒2)²]
|PQ| = √[(‒2)² + 4² + 2²]
|PQ| = √[4 + 16 + 4] = √24

Panjang RQ:
|RQ| = √[(‒1‒2)² + (0‒(‒3))² + (2‒2)²]
|RQ| = √[(‒3)² + 3² + 0²]
|RQ| = √[9 + 9 + 0] = √18

Misalkan ∠PQR = θ
Menghitung besar sudut PQR:
|PR|² = |PQ|² + |RQ|² ‒ 2·|PQ|·|RQ|· cos θ
6 = 24 + 18 ‒ 2·√24·√18· cos θ
2√432 · cos θ = 24 + 18 ‒ 6
24√3 · cos θ = 36
cos θ = ³⁶/_24√3 × ^√3/_√3
cos θ = ^36√3/₇₂
cos θ = ¹/₂√3 → θ = 30^o

Jadi, besar sudut PQR adalah 30^o.

Cara lain:

Besar sudut PQR juga dapat dicari dengan rumus besar sudut antara dua vektor.

Pada soal diketahui segitiga PQR dengan P(0 1 4), Q(2, ‒3, 2), dan R (‒1, 0, 2).

Pada segitiga PQR, sudut PQR adalah sudut antara vektor QP dan QR. Pertama akan tentukan koordinat vektor QP dan QR serta panjang kedua vektor tersebut.

QP = P ‒ Q
= (0‒2, 1‒(‒3), 4‒2)
= (‒2, 4, 2)

|QP| = √{(‒2)² + 4² + 2²}
= √(4+16+4) = √24

QR = R ‒ Q
= (‒1‒2, 0‒(‒3), 2‒2)
= (‒3, 3, 0)

|QP| = √{(‒3)² + 3² + 0²}
= √(9+9+0) = √18

Misalkan besar ∠PQR = θ
Menghitung besar sudut PQR:

Cos θ = ¹⁸/_√(144×3)
Cos θ = ¹⁸/_12√3 × ^√3/_√3
Cos θ = ^18√3/₃₆
Cos θ = ¹/₂√3 → θ = 30^o

Sehingga, untuk diketahui segitiga PQR dengan P(0 1 4), Q(2, -3, 2), dan R (-1, 0, 2). Besar sudut PQR adalah θ = 30^o.