Luas daerah parkir 1.760 m2. Luas rata-rata untuk mobil kecil 4 m2 dan mobil besar 20 m2 daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil Rp1.000/jam dan mobil besar Rp2.000/jam.
Jika dalam 1 jam terisi penuh dan tidak ada kendaraan yang pergi dan datang, hasil maksimum tempat parkir itu adalah ….
A. Rp176.000,00
B. Rp200.000,00
C. Rp260.000,00
D. Rp300.000,00
E. Rp340.000,00
Jawab: C
Secara ringkas, langkah menyelesaikan soal program linear terdapat pada beberapa nomor di bawah.
- Membuat model matematika yang sesuai dengan soal yang diberikan.
- Menentukan daerah layak
- Menentukan titik pojok dari daerah layak
- Menghitung nilai fungsi tujuan untuk menentukan nilai minimum/maksimum, tergantung dari soal yang diberikan.
Pertama, kita perlu memodelkan soal certia sehingga dapat diperoleh fungsi kendala dan fungsi tujuan. Untuk memodelkan soal cerita, gunakan pemisalan variabel seperti cara berikut.
Misalkan:
x = banyaknya mobil kecil
y = banyaknya mobil besar
Informasi pada soal:

Tabel di atas dapat memudahkan kita untuk membentuk fungsi tujuan dan fungsi kendala seperti berikut.
Fungsi tujuan:
Memaksimalkan f(x, y) = 1.000x + 2.000y
Fungsi kendala:
(i) x + y ≤ 200
(ii) 4x + 20y ≤ 1.760
(iii) x ≥ 0; (iv) y ≥ 0
Daerah yang memenuhi fungsi kendala:

Untuk titik koordinat A, B, dan D dapat secara mudah diketahui dengan mengamati diagram gambar di atas. Sedangkan koordinat titik C dapat diketahui dengan mencari titik potong antara dua garis yaitu (i) x + y ≤ 200 dan (ii) 4x + 20y ≤ 1.760 seperti yang dilakukan pada penyelesaian berikut
Menentukan titik ordinat (y) untuk titik C:
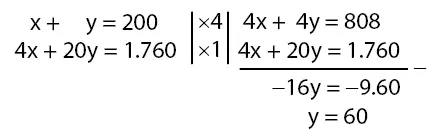
Menentukan titik absis (x) untuk titik C:
x + y = 200
x + 60 = 200
x = 200 ‒ 60 = 140
Diperoleh titik perpotongan antara garis (i) x + y ≤ 200 dan (ii) 4x + 20y ≤ 1.760 adalah C(140, 60).
Selanjutnya akan dicari nilai maksimum yang dihasilkan fungsi tujuan dengan metode titik. Caranya adalah substitusi nilai (x, y) pada persamaan fungsi tujuan f(x, y) = 1.000x + 2.000y seperti yang dilakukan pada cara berikut.
| Titik | Nilai fungsi tujuan f(x, y) = 1.000x + 2.000y |
| A(0, 0) | f(0,0) = 1.000×0 + 2.000×0 = 0 |
| B(0, 88) | f(0,00) = 1.000×0 + 2.000×88 = 176.000 |
| C(140, 60) | f(140, 60) = 1.000×140 + 2.000×60 = 260.000 |
| D(200, 0) | f(200,0) = 1.000×200 + 2.000×0 = 200.000 |
Diperoleh nilai fungsi tujuan paling besar di titik C (140, 60). Jadi, jika dalam 1 jam terisi penuh dan tidak ada kendaraan yang pergi dan datang, maka hasil maksimum tempat parkir itu adalah Rp260.000,00.