Jika A−1 = Bt dengan A−1 adalah invers matriks A dan Bt adalah transpose matriks B maka nilai a − b = ….

Jika A⁻¹ = B^t dengan A⁻¹ adalah invers matriks A dan B^t adalah transpose matriks B maka nilai a − b = ….
A. 3
B. 2
C. 1
D. −2
E. −3

Jawab: A

Invers matriks adalah sebuah matriks baru yang merupakan kebalikan dari matriks asalnya. Perkalian antara matriks asal dan invers matriksnya selalu menghasilkan matriks identitas.

Elemen-elemen dari matriks baru yang menjadi invers matriks merupakan hasil operasi elemen matriks asalnya. Cara menentukan invers matriks A dilakukan dengan langkah penyelesaian berikut.

Menentukan invers matriks A:

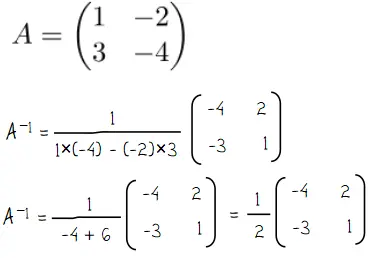
Transpose matriks adalah suatu matriks baru yang diperoleh dengan cara menukarkan elemen baris dan kolom. Cara menentukan transpose matriks B dilakukan seperti langkah penyelesaian berikut.

Menentukan transpose matriks B:

Diketahui A⁻¹ = B^t sehingga dapat dibentuk persamaan berikut untuk mengetahui nilai a + b.

Dari persamaan matriks di atas dapat diperoleh persamaan (i) a = ¹/₂ dan persamaan (ii) a + b = −2. Substitusi nilai a = ¹/₂ pada persamaan a + b = −2 untuk mendapatkan nilai b.

Menghitung nilai b:
a + b = −2
¹/₂ + b = −2
b = −2 − ¹/₂ = −2¹/₂

Menghitung nilai a − b:
a − b = ¹/₂ − (−2¹/₂)
a − b = ¹/₂ + 2¹/₂
a − b = 3

Jadi, nilai a + b adalah 3.