Jika f(x) = x + 2 dan g(x) = 3 – x/2x + 1 maka (f o g)^‒1(x) = ….

Jika f(x) = x + 2 dan g(x) = 3 – x/2x + 1 maka (f o g)^‒1(x) = ….
A. ^{x ‒ 5}/_{3 ‒ 2x}
B. ^{x ‒ 5}/_{2x ‒ 3}
C. ^{x + 5}/_{2x ‒ 3}
D. ^{x ‒ 5}/_{2x + 3}
E. ^{2x ‒ 3}/_{x + 5}

Jawab: A

Simbol matematis untuk (fog)^‒1(x) digunakan untuk menyatakan invers dari fungsi (fog)(x). Sehingga, untuk mengetahui persamaan (fog)^‒1(x) perlu mengetahui fungsi komposisi (fog)(x) terlebih dahulu.

Diketahui fungsi f(x) dan g(x):

• f(x) = x + 2
• g(x) = ^{3 – x}/_{2x + 1}

Menentukan (f o g)(x):
(f o g)(x) = f(g(x)) = f(^{3 – x}/_{2x + 1})

Fungsi komposisi memiliki bentuk umum ^{ax + b}/_{cx + d} yaitu (f o g)(x) = ^{5 + 3x}/_{2x + 1}. Fungsi invers dari persamaan dengan bentuk umum y = ^{ax + b}/_{cx + d} dapat diketahui cara cepat mencari fungsi invers seperti cara berikut.

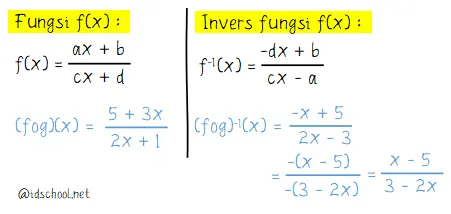
Jadi, jika f(x) = x + 2 dan g(x) = 3 – x/2x + 1 maka (f o g)^‒1(x) = ^{x – 5}/_{3 – 2x}.