Jika ditik P terletak pada tengah-tengah garis BF maka jarak antara titik A dan P adalah ….

Diketahui sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Jika titik P terletak pada tengah-tengah garis BF maka jarak antara titik A dan P adalah ….
A. 5√3 cm
B. 5√2 cm
C. 3√7 cm
D. 3√5 cm
E. 3√3 cm

Jawab: D

Gambar kubus yang sesuai dengan keterangan yang diberikan pada soal adalah sebagai berikut. 

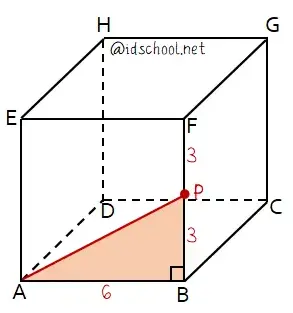
Perhatikan bahwa titik P dengan titik A dan B membentuk segitga ABP. Segitiga siku-siku APB adalah segitiga siku-siku dengan sudut siku-siku di titik B.

Pada segitiga siku-siku berlaku persamaan yang sesuai Teorema Pythagoras. Sehingga panjang AP dapat dihitung dengan rumus Phytagoras seperti cara penyelesaian berikut.

Menghitung panjang AP:
AP² = 6² + 3²
AP² = 36 + 9 = 45
AP = √45 = √(9×5)
AP = √9×√5 = 3√5 cm

Jadi, jarak antara titik A dan P adalah AP = 3√5 cm.