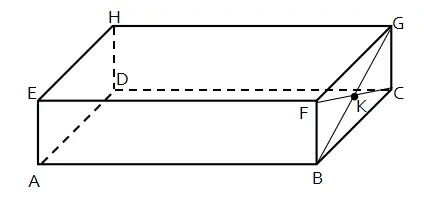
Pada balok ABCD.EFGH, AB = 6, AD = 4, dan AE = 2. Titik K adalah titik potong diagonal bidang BCGF.

Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?

(A) Kuantitas P lebih besar daripada Q

(B) Kuantitas P lebih kecil daripada Q

(C) Kuantitas P sama dengan Q

(D) Tidak dapat ditentukan hubungan antara kuantitas P dan Q.

Jawab: (B)

Jarak titik ke titik pada dimensi tiga sama dengan panjang ruas garis yang menghubungkan kedua titik tersebut. Sehingga jarak titik K ke D adalah panjang ruas garis KD seperti yang terdapat pada gambar di bawah.

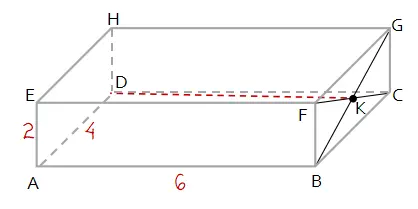
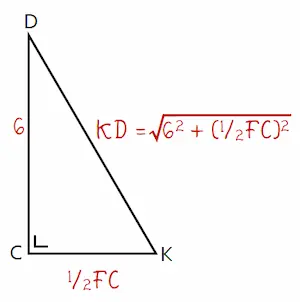
Diperoleh bentuk sebuah segitiga DCK, di mana ΔDCK merupakan segitga siku-siku di titik C. Sehingga panjang ruas garis KD dapat dihitung menggunakan Teorma Pythagoras seperti berikut.

Menghitung panjag FC:

FC = √(4² + 2²)

FC = √(16 + 4) = √20

FC = √(4×5) = 2√5

Menghitung panjang KD:

KD = √(6² + (¹/₂×2√5)²)

KD = √(6² + (√5)²)  

KD = √(36 + 5) = √41

Diperoleh panjang KD = √41, sehingga jarak dari K ke D sama demgan √41. Dengan demikian besar P = jarak dari K ke D = √41 dan Q = √61. Jadi, hubungan antara kuantitas P dan Q berikut yang benar adalah kuantitas P lebih kecil dari Q.