Energi kinetik adalah sejumlah energi yang terdapat pada benda yang bergerak. Sebuah benda yang bergerak pada suatu lintasan dengan gerak berubah beraturan memiliki energi kinetik yang berbeda pada setiap titik. Perbandingan kuadrat kecepatan benda pada titik yang berbeda sama dengan perbandingan energi kinetik benda tersebut. Sehingga, dengan mengetahui nilai kecepatan benda antara dua titik dapat diketahui pula perbandingan energi kinetik pada dua titik tersebut.
Bagaimana cara menentukan perbandingan energi kinetik suatu benda pada dua titik yang berbeda? Apa rumus energi kinetik dari suatu benda yang bergerak? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Besar Energi Kinetik
Besar kecilnya energi kinetik dipengaruhi oleh kecepatan dari kecepatan gerak suatu benda. Benda yang bergerak dengan kecepatan semakin tinggi memiliki energi kinetik yang semakin besar. Sebaliknya, benda yang bergerak dengan kecepatan rendah memiliki energi kinetik yang semakin kecil.
Besar energi kinetik dapat dihitung melalui rumus Ek = ½mv2. Di mana m adalah massa benda dan v adalah kecepatan gerak benda.

Persamaan rumus energi kinetik di atas menunjukkan bahwa besar energi kinetik berbanding senilai dengan massa dan kecepatan gerak benda.
Baca Juga: Rumus Energi Potensial, Energi Kinetik, dan Energi Mekanik
Perbandingan Energi Kinetik
Sebuah benda yang bergerak dengan kecepatan berubah beraturan pada suatu lintasan memiliki energi kinetik yang berbeda di setiap titik. Misalnya pada sebuah benda bermassa m yang dijatuhkan dari suatu ketinggian h. Pada awalnya, benda tersebut dalam keadaan diam atau nilai v = 0. Pada benda dengan kecepatan gerak benda v = 0, nilai energi kinetiknya juga sama dengan nol (Ek = 0).
Setelah benda tersebut jatuh sesaat, benda akan mulai bergerak dengan kecepatan tertentu. Karena benda jatuh bebas ke bawah maka kecepatan gerak benda akan semakin cepat sehingga energi kinetiknya semakin besar. Perbandingan energi kinetik pada titik berbeda dapat dilakukan dengan cara membandingkan kedua nilai energi kinetiknya.
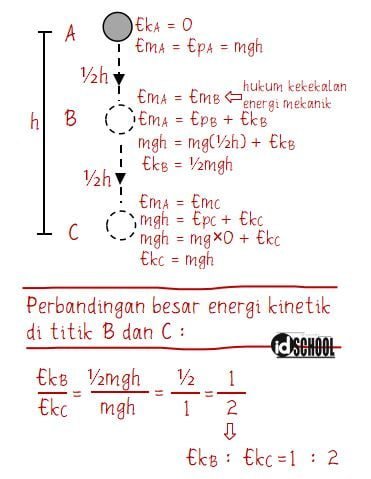
Selanjutnya, sobat idschool dapat melihat beberapa bentuk soal mengenai perbandingan energi kinetik.
Baca Juga: Energi Kinetik Gas Ideal
Contoh Soal dan Pembahasan
Beberapa soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkpai dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Perbandingan Energi Kinetik Ek1 : Ek2

Pembahasan:
Berdasarkan keterangan yang diberikan pada soa dapat diperoleh informasi-informasi seperti berikut.
- Massa benda pertama: m1 = 5 kg
- Massa benda kedua: m2 = 15 kg
- Ketinggian benda posisi pertama (di titik A): hA = 40 cm
- Ketinggian benda posisi kedua (di titik B): hB = 30 cm
Benda pada titik A awalnya belum bergerak (v = 0) sehingga energi kinetik (Ek) kedua benda tersebut sama dengan nol (Ek = ½×m×v2=½×m×02=0). Sehingga, energi mekanik kedua benda pada titi A sama dengan energi potensialnya karena EmA= EpA+EkA= EpA+0 =EpA.
Dengan demikian, energi mekanik benda pertama dan kedua di titik A seperti hasil perhitungan di bawah.
- Energi mekanik benda pertama di titik A:
EmA1 = EpA1
EmA1 = m1×g×hA
= 5×10×40
= 2.000 joule
- Energi mekanik benda kedua di titik A:
EmA2 = EpA2
EmA2 = m2×g×hB
= 15×10×40
= 6.000 joule
Selanjutnya, pada titik B berlaku hukum kekekalan energi mekanik yaitu energi mekanik di titik A sama dengan di titik B (EmA=EmB). Sehingga dapat diperoleh besar energi kinetik pada kedua benda tersebut.
- Energi kinetik benda pertama di titik B:
EmA1 = EmB1
EmA1 = EpB1+EkB1
2.000 = m1×g×hB + EkB1
2.000 = 5×10×30 + EkB1
EkB1 = 2.000−1.500 = 500 joule
- Energi mekanik benda kedua di titik B:
EmA2 = EmB2
EmA2 = EpB2 + EkB2
6.000 = m2×g×hB+EkB2
6.000 = 15×10×30+EkB2
EkB2 = 6.000−4.500=1.500 joule
Jadi, perbandingan energi kinetik di titik B adalah EkB1 : EkB2 = 500 : 1.500 = 1 : 3.
Jawaban: B
Contoh 2 – Menentukan Ketinggian Benda dari Keterangan Perbandingan Energi Kinetik pada Dua Titik yang Berbeda
Sebuah benda jatuh bebas dari ketinggian tertentu. Jika energi kinetik di titik A adalah seperempat kali energi kinetik di titik B maka perbandingan tinggi benda saat di titik A dan B adalah ….
A. 1 : 4
B. 1 : 2
C. 2 : 1
D. 4 : 1
E. 8 : 1
Pembahasan:
Keterangan pada soal memberikan informasi bahwa energi kinetik di titik A adalah seperempat kali energi kinetik di titik B (EkA = ¼EkB). Dengan demikian dapat diperoleh persamaan ½mvA2 = ¼×½mvB2. Dari persamaan tersebut dapat diperoleh persamaan vA2 = ¼vB2 karena massa beda sama di setiap titik.
Ingat bahwa kecepatan (v) benda dapat dihitung melalui persamaa v2 = 2gh. Misalkan ketinggian benda di titik A adalah hA dan ketinggian benda di titik B adalah hA. Substitusi nilai vA2 = 2ghA dan vB2 = 2ghB akan menghasilkan perbandingan ketinggian di titik A dan B seperti diberikan pada perhitungan di bawah.
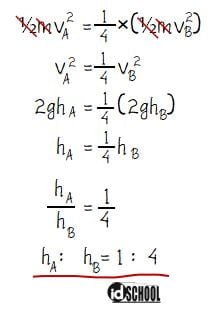
Jadi, perbandingan tinggi benda saat di titik A dan B adalah hA : hB = 1 : 4.
Jawaban: A
Contoh 3 – Perbandingan Energi Kinetik dan Kecepatan Dua Benda
Bola A bermassa 500 gram dilepaskan menempuh lintasan seperti gambar berikut.

Lintasan AB adalah seperempat lingkaran licin dengan jari-jari h cm. Jika selisih ketinggian titik B dan C adalah h cm maka perbandingan kecepatan bola di titik B dan C adalah ….
A. 1 : √2
B. 1 : 2
C. √2 : 1
D. √2 : 2
E. √2 : 3
Pembahasan:
Hukum kekekalan energi mekanik pada setiap titik adalah sama sehingga EmA = EmB = EmC. Diketahui benda mulai bergerak dari titik A sehingga kecepatan benda pada titik A adalah 0 (vA = 0). Dengan demikian energi mekanik di titik A sama dengan energi potensialnya karena EkA = ½mvA2 = = ½m · 02 = 0.

Jadi, perbandingan kecepatan bola di titik B dan C adalah 1 : √2.
Jawaban: A
Demikianlah tadi ulasan cara menentukan perbandingan energi kinetik dua benda, serta contoh soal dan pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Besar Usaha dan Efisiensi Mesin Carnot