Rumus ANOVA berupa kumpulan rumus hitung yang terdiri dari sum of square, degree of freedom, mean square, dan F value. Beberapa komponen dalam rumus ANOVA tersebut diberikan dalam sebuah tabel yang disebut tabel ANOVA. Penggunaan tabel dan rumus ANOVA dilakukan untuk mempermudah perhitungan dalam melakukan uji statistik untuk data kelompok.
ANOVA sendiri merupakan suatu kependekan, di mana kepanjangan ANOVA adalah Analysis of Variance (analisis ragam). Uji ANOVA merupakan salah satu bentuk alat analisis uji signifikansi yang digunakan pada data kelompok. Di mana uji signifikansi statistik digunakan untuk mengambil kesimpulan apakah Null Hypotesis atau Hipotesis Nol ditolak atau diterima pada saat pengujian.
Uji sifnifikansi dilakukan dengan cara membandingkan nilai f hitung dengan f tabel. Nilai f hitung diperoleh dari tabel dan rumus ANOVA. Sedangkan nilai f tabel diperoleh dengan melihat tabel f yang menunjukan nilai kritis titik persentase distribusi dengan suatu taraf kepercayaan.
Nilai f hitung menjadi bagian yang dilihat dalam uji ANOVA, bagaimana proses mendapatkan nilai f hitung? Apa saja persamaan dalam rumus ANOVA? Bagaimana bentuk tabel ANOVA? Bagaimana cara melakukan uji ANOVA? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Uji ANOVA
- One-Way ANOVA atau ANOVA 1 Arah
- Tabel dan Rumus ANOVA 1 Arah
- Contoh Penggunaan Uji ANOVA 1 Arah
Baca Juga: Contoh Analisis Statistik Deskriptif
Uji ANOVA
Uji ANOVA disebut juga uji serentak atau uji F yaitu salah satu metode analisis statistik menguji perbedaan rata-rata antar kelompok dengan jenis perlakuan berbeda. Di mana uji ANOVA digunakan untuk melihat bagaimanakah pengaruh semua variabel bebas terhadap variabel terikatnya secara bersama-sama.
Tujuan penggunaan uji ANOVA adalah untuk menganalisis keragaman dalam kelompok serta keragaman di antara kelompok. Ada dua macam uji ANOVA berdasarkan jumlah variabel bebas yang diteliti yaitu One-Way ANOVA dan Two-Way ANOVA.
One way ANOVA atau ANOVA 1 arah digunakan untuk data dengan banyak variabel bebas sama dengan satu. Sedangkan uji ANOVA untuk data dengan dua atau lebih variabel bebas menggunakan Two-Way ANOVA (ANOVA 2 Arah).
Fokus bahasan di bawah adalah rumus ANOVA 1 arah, sementara untuk ANOVA 2 arah terdapat pada bahasan halaman Two-Way ANOVA.
One-Way ANOVA atau ANOVA 1 Arah
Hipotesis pada one way ANOVA yang dapat dibentuk berupa Null Hypothesis (H0) dan Alternative Hypothesis (H1). Bentuk hipotesis pada one way ANOVA secera umum sesuai dengan dua pernyataan berikut.
Hipotesis:
H0: μ1 = μ2 = μ3 = … = μn
H1: Rata-rata kelompok tidak sama
Pengambilan keputusan dari uji statistik pada one way ANOVA adalah menolak H0 ketika tes statistik (f hitung) lebih besar dari nilai kritis tabel F dengan suatu signifikansi α. Sedangkan saat diperoleh f hitung lebih kecil dari nilai kritis tabel F dengan signifikansi α maka keputusan yang diambil adalah menerima H0.

Proses pengerjaan uji ANOVA secara umum terdapat pada tahapan atau langkah-langkah berikut.
- Hitung rata-rata setiap kelompok
- Hitung rata-rata data untuk ketiga kelompok
- Melakukan perhitungan jumlah kuadrat atau sum of square (SSB, SSE, dan SST)
- Menentukan nilai derajat bebas atau degress of freedom (df1 dan df2)
- Melakukan perhitungan kuadrat tengah atau mean square (MSB dan MSE)
- Mencari tes statistik f hitung
- Mencari nilai kritis f tabel dengan signifikansi α serta derajat bebas v1 = df1 dan v2 = df2
Baca Juga: Contoh Pengerjaan Analisis Regresi Linear Sederhana dengan Perhitungan Manual
Tabel dan Rumus ANOVA 1 Arah
Ada beberapa langkah perhitungan yang dilakukan pada perhitungan dalam tabel ANOVA. Akhir dari perhitungan dari rumus ANOVA adalah mendapatkan nilai f hitung. Di mana nilai f hitung digunakan pada uji signifikansi dengan cara membandingkannya nilainya dengan nilai pada f tabel.
Langkah perhitungan yang dilakukan dalam hasil uji ANOVA diringkas dalam sebuah tabel ANOVA. Dalam tabel ANOVA memuat rumus hitung untuk jumlah kuadrat (sum of square), derajat kebebasan (degrees of freedom), rata-rata kuadrat (mean square), dan f hitung (f value). Bentuk tabel dan rumus ANOVA sesuai dengan tabel berikut.
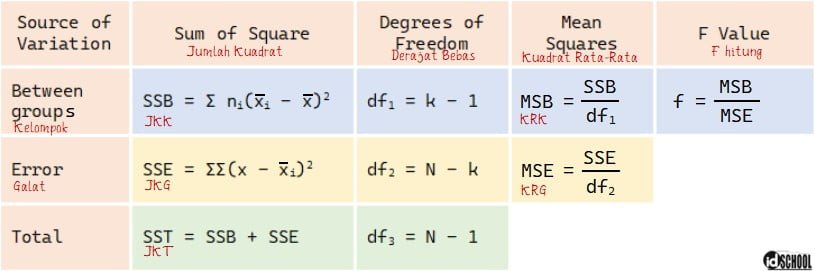
Keterangan simbol yang diberikan pada tabel dan rumus ANOVA diberikan pada penjelasan berikut.
_
xi = rata-rata kelompok ke-i
_
x = rata-rata dari semua data
xi = data ke-i
ni = banyak data pada kelompok ke-i
N = jumlah semua data
k = banya kelompok
Baca Juga: Contoh Klasifikasi kNN dengan Python
Contoh Penggunaan Uji ANOVA 1 Arah
Sebuah percobaan dilakukan menggunakan 3 jenis pupuk berbeda yang diberikan pada tiga kelompok tanaman selama 5 minggu. Dari percobaan tersebut akan diselidiki apakah ada perbedaan rata-rata pertumbuhan pada setiap kelompok.
Data rata-rata pertumbuhan tanaman untuk tiga kelompok terdapat pada tabel berikut.
| Pupuk 1 | Pupuk 2 | Pupuk 3 |
| 6 | 8 | 13 |
| 8 | 12 | 9 |
| 4 | 9 | 11 |
| 5 | 11 | 8 |
| 3 | 6 | 7 |
| 4 | 8 | 12 |
Penyelesaian:
Langkah pertama dalam melakukan uji ANOVA adalah menentukan hipotesis. Selanjutnya dilakukan perhitungan dengan tabel dan rumus ANOVA untuk melakukan uji serentak.
Hipotesis:
H0: μ1 = μ2 = μ3
H1: rata-rata kelompok tidak sama
Dari data pada tabel dapat diketahui bahawa banyak datum untuk setiap kelompok adalah n = n1 = n2 = n3 = 6, k = banyak kelompok = 3, dan N = banyak datum = 18.
Rata-rata untuk setiap kelompok 1, 2, dan 3 dicari seperti cara berikut.
- Rata-rata kelompok 1 = 6+8+4+5+3+4/6 = 30/6 = 5
- Rata-rata kelompok 2 = 8+12+9+11+6+8/6 = 54/6 = 9
- Rata-rata kelompok 3 = 13+9+11+8+7+12/6 = 60/6 = 10
Menghitung rata-rata untuk 3 kelompok:
_
x = 5 + 9 + 10/3
_
x = 24/3 = 8
Jumlah kuadrat kelompok:
SSB = 6(5 ‒ 8)2 + 6(9 ‒ 8)2 + 6(10 ‒ 8)2
SSB = 6×(‒3)2 + 6×12 + 6×22
SSB = 6×9 + 6×1 + 6×4
SSB = 54 + 6 + 24
SSB = 84
Untuk menghitung jumlah kuadrat error (Sum of Square Error atau SSE) dapat dilakukan dengan cara berikut.

Menghitung SSE:
SSE = 16 + 24 + 28
SSE = 68
Menghitung derajat bebas:
df1 = k ‒ 1 = 3 ‒ 1 = 2
df2 = N ‒ k = 18 ‒ 3 = 15
df3 = N ‒ 1 = 18 ‒ 1 = 17
Beberapa perhitungan yang dilakukan dengan rumus ANOVA di atas dapat dimuat dalam bentuk tabel ANOVA berikut.

Dari hasil perhitungan menggunakan tabel dan rumus ANOVA diperoleh nilai fhitung = 9,26. Sementara untuk f tabel dapat dilihat melalui tabel f dengan tingkat signifikansi α = 0,05 (selang kepercayaan 95%). Nilai titik kritis untuk F dengan signifikansi α = 0,05 serta derajat kebebasan df1 = 2 dan df2 = 15 adalah F(α=0,05; 2; 15) = 3,68.

Kerena nilai f hitung besar dari f tabel (fhitung > F) maka hipotesis nol (H0) ditolak atau signifikan. Sehingga dapat disimpulkan bahwa ada perbedaan pertumbuhan tanaman karena pengaruh pemberian pupuk.
Jika pada uji ANOVA diperoleh kesimpulan tidak signifikan maka tidak perlu dilakukan uji lanjut karena kesimpulan sudah final (tidak ada perbedaan yang signifikan). Jika pada uji ANOVA diperoleh kesimpulan signifikan maka dapat dilakukan uji lanjut.
Demikianlah tadi ulasan uji ANOVA yang dilakukan dengan perhitungan manual (tanpa alat bantu) menggunakan tabel dan rumus ANOVA. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Mengerjakan Statistika Deskriptif dengan Google Sheets