Two-way ANOVA atau ANOVA dua arah merupakan salah satu bentuk alat tes statisik untuk uji signifikansi. Tabel two way ANOVA digunakan untuk menganalisis data kelompok dengan banyak variabel bebas lebih dari satu. Dalam tabel ANOVA dua arah terdapat rumus hitung untuk menghitung jumlah kuadrat, derajat bebas, kuadrat rata-rata, dan nilai f hitung.
Bagaimana bentuk rumus dan tabel ANOVA dua arah? Bagaimana cara mengerjakan uji ANOVA dua arah? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Tabel ANOVA Dua Arah dan Rumusnya
Tabel ANOVA dua arah memuat rumus-rumus perhitungan yang terdiri dari degrees of freedoms (df), sum of square (SS), mean square (MS), dan f value. Untuk keterangan rumus dalam Bahasa Indonesia secara urut adalah derajat bebas (db), jumlah kuadrat (JK), kuadrat rata-rata (KR), dan f hitung.
Beberapa sumber menggunakan keterangan dalam Bahasa Inggris, beberapa sumber lain bisa menggunakan Bahasa Indonesia. Namun tidak ada perbedaan rumus antara keduanya, yang berbeda hanya penyimbolannya saja.
Penggunaan rumus dan tabel ANOVA dua arah untuk menguji hipotesis komparatif rata-rata beberapa sampel dalam beberapa kategori (kelompok) dengan beberapa perlakukan. Untuk penelitian dengan banyak blok b = 3 dan banyak perlakuan k = 6, data dapat disajikan dalam tabel yang terdiri 3 baris (blok) dan 6 kolom (perlakuan). Gambaran data yang sesuai untuk bentuk penelitian tersebut terdapat pada keterangan berikut.
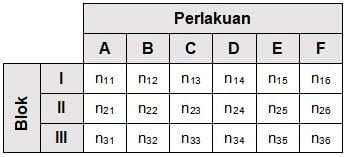
Baca Juga: Tabel dan Rumus ANOVA 1 Arah (One-Way ANOVA)
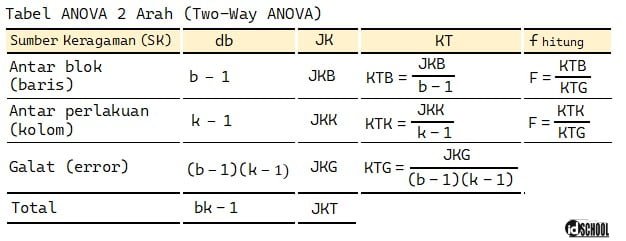
Pada One Way ANOVA, sumber keragaman adalah perlakukan kelompok dan galat (error). Sedangkan pada Two Way ANOVA sumber keragaman pada perlakukan, blok, dan galat. Kumpulan rumus hitung dan bentuk tabel ANOVA dua arah sesuai dengan tabel dan rumus hitung berikut.

Baca Juga: Analisis Regresi Linear Sederhana
Langkah Uji ANOVA Dua Arah
Akhir dari proses hitung dengan rumus dan tabel ANOVA dua arah adalah mendapatkan nilai f hitung sebagai uji signifikansi. Untuk langkah-langkah yang dikerjakan dalam perhitungan ANOVA dua arah secara umum terdapat pada tahapan berikut.
- Identifikasi nilai: t (jumlah perlakuan) dan r (jumlah blok)
- Hitung jumlah pengamatan total (n): n = p × b
- Menentukan derajat bebas (degree of freedoms)
- Menghitung jumlah kuadrat (sum of square)
- Menghitung jumlah kuadrat perlakuan dengan rumus:
- Hitung jumlah kuadrat antar blok dengan rumus:
- Mendapatkan nilai f hitung
- Mencari nilai f tabel yang sesuai dengan tingkat signifikansi (α) yang ditetapkan
- Menarik kesimpulan
Penarikan kesimpulan pada Uji ANOVA dua arah dilakukan dengan membandingkan nilai f hitung dan f tabel. Penarikan kesimpulan digunakan untuk menentukan hipotesis dari penelitian. Hipotesis adalah dugaan sementara yang akan diuji melalui sebuah penelitian.
Bentuk Hipotesis pada Uji ANOVA 2 Arah
Hipotesis yang digunakan pada ANOVA dua arah adalah bergantung dari berapa banyak faktor yang ditelititi. Misalnya pada penelitian dengan dua faktor yang memengaruhi (variabel bebas) maka hipotesis penelitian secara umum memiliki bentuk seperti berikut.
- Hipotesis untuk faktor pertama:
H0: α1 = α2 = … = αn (Tidak ada perbedaan rata-rata (mean) yang signifikan dalam kategori faktor pertama)
H1: αi ≠ αj (Terdapat perbedaan rata-rata (mean) yang signifikan dalam kategori faktor pertama)
- Hipotesis untuk faktor kedua:
H0: β1 = β2 = … = βn (Tidak ada perbedaan rata-rata (mean) yang signifikan dalam kategori faktor kedua)
H1: βi ≠ βj (Terdapat perbedaan rata-rata (mean) yang signifikan dalam kategori faktor kedua)
Kriteria penarikan kesimpulan dari hipotesis sesuai dengan dua kondisi berikut.
- f hitung < F tabel → H0 diterima
Kesimpulan: Tidak ada perbedaan yang signifikan pada rata-rata antar perlakuan - f hitung ≥ F tabel → Ho ditolak
Kesimpulan: : Terdapat perbedaan yang signifikan pada rata-rata antar perlakuan
Baca Juga: Perbedaan Penelitian Kualitatif dan Kuantitatif
Contoh Penggunaan Rumus dan Tabel ANOVA Dua Arah
Seorang peneliti ingin mengetahui bagaimana pengaruh usia untuk suatu metode diet terhadap penurunan berat badan. Penelitian dilakukan pada empat metode diet yaitu metode I, II, III, dan IV. Dalam penelitian tersebut menggunakan tiga kelompik usia yaitu kurang dari 20 tahun (< 20 tahun), antara 20 tahun samapi 40 tahun (20 ‒ 40 tahun), dan lebih dari 40 tahun (> 40 tahun).
Penelitian disusun berdasarkan desaian rancangan acak kelompok dan rata-rata penurunan berat badan (dalam kg) yang menjadi parameter. Setelah dilakukan pengukuran terhadap rata-rata penurunan untuk tiga kelompok usia dengan empat metode diet diperoleh data seperti tabel berikut.
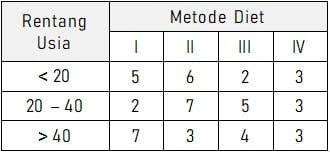
Untuk mengetahui apakah ada perbedaan signifikan antar perlakuan, maka dilakukan uji ANOVA dua arah. Sebelum bentuk hipotesis yang akan diujikan terlebih dahulu.
- Hipotesis untuk faktor rentang usia (baris):
H0: α1 = α2 = α3 (tidak ada perbedaan rata-rata penurunan berat badan dalam kategori rentang usia)
H1: αi ≠ αj (setidaknya ada satu rata-rata penurunan berat badan yang berbeda dalam kategori rentang usia)
- Hipotesis untuk faktor metode diet (kolom):
H0: β1 = β2 = β3 (tidak ada perbedaan rata-rata penurunan berat badan dalam kategori metode diet)
H1: βi ≠ βj (setidaknya ada satu rata-rata penurunan berat badan yang berbeda dalam kategori metode diet)
Dari data pada tabel dapat diketahui banyak kelompok (baris), banyak perlakuan atau metode (kolom), dan jumlah data yaitu,
- Banyak blok (baris): b = 3
- Banyak perlakuan (kolom): k = 4
- Banyak datum: n = b×k = 3×4 = 12
- Menentukan degrees of freedoms (df) atauderajat bebas (db):
db1 = b ‒ 1 = 3 ‒ 1 = 2
db2 = k ‒ 1 = 4 ‒ 1 = 3
Dengan beberapa informasi yang diperoleh maka dapat dibentuk sebuah tabel ANOVA dua arah yang belum selesai seperti berikut.
| Sumber | db | JK | KT | f hitung |
| Rentang usia | 2 | JKB | KTB = JKB/2 | f = KTB/KTG |
| Metode diet | 3 | JKK | KTK = JKK/3 | f = KTK/KTG |
| Galat (error) | 6 | JKG | KTG = JKG/6 | |
| Total | 11 | JKT |
Nilai JK, KT, dan f hitung dalam tabel ANOVA dua arah di atas belum diketahui karena belum dilakukan perhitungan untuk nilai-nilai tersebut. Sehingga perlu dilakukan untuk menentukan nilai-nilai tersebut seperti beberapa langkah perhitungan yang dikerjakan berikut.
Menghitung Sum of Square (SS) atau jumlah kuadrat (JK) untuk blok (JKB), perlakuan (JKK), dan galat (JKG). Proses perhitungan JKB, JKK, dan JKG dilakukan seperti proses pengerjaan berikut.

Selanjutnya nilai JKB, JKK, JKT, dan JKG dapat dihitung dengan cara substitusi nilai-nilai yang sesuai ke rumus. Cara menghitung nilai-nilai jumlah kuadrat dilakukan seperti beberapa cara penyelesaian berikut.
1) Menghitung jumlah kuadrat baris:

2) Menghitung jumlah kuadrat kolom:

3) Menghitung jumlah kuadrat total:
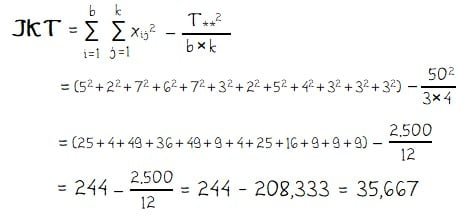
4) Menghitung jumlah kuadrat galat:
JKG = JKT ‒ JKB ‒ JKK
JKG = 35,667 ‒ 0,167 ‒ 9,667
JKG = 25,833
Dari nilai JKB, JKK, JKT, dan JKG selanjutnya dapat digunakan untuk menghitung mean square (MS) atau kuadrat tengah untuk blok (KTB), perlakuan (KTK), dan galat (KTG). Selanjutnya nilai ketiga kuadrat tengah tersebut dapat digunakan untuk mendapatkan nilai f hitung dalam tabel ANOVA dua arah seperti berikut.
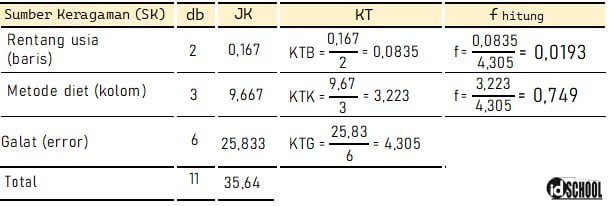
Pada hasil uji ANOVA dua arah diatas diperoleh nilai f hitung untuk faktor kelompok usia adalah fhitung (usia) = 0,0193 dan nilai f hitung untuk faktor metode diet adalah fhitung (metode) = 0,749.
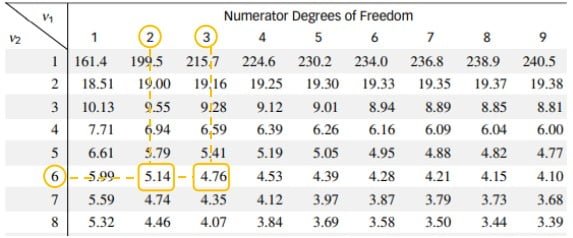
Untuk nilai F tabel, Nilai kritis dengan F(α=0,05; 2; 6) dapat dilihat melalui tabel distribusi F yang mencantumkan nilai F tabel = 5,14. Nilai kritis dengan F(α=0,05; 3; 6) dapat dilihat melalui tabel distribusi F yang mencantumkan nilai F tabel = 4,76.
Terakhir adalah melakukan penarikan kesimpulan dengan cara membandingkan nilai f hitung yang diperoleh pada tabel ANOVA dua arah dan nilai f tabel. Penarikan kesimpulan dilakukan menggunakan nilai f hitung dan f tabel yang sesuai untuk kategori rentang usia dan metode diet.
- Untuk faktor rentang usia:
fhitung (usia) = 0,0913
F(α=0,05; 2; 6) = 5,14
Keputusan: fhitung (usia) < F → H0 diterima (H0: α1 = α2 = α3)
Kesimpulan: Tidak ada perbedaan rata-rata penurunan berat badan yang dignifikan dalam kategori rentang usia
- Untuk faktor metode diet:
fhitung (usia) = 0,749
F(α=0,05; 3; 6) = 4,76
Keputusan: fhitung (usia) < F → H0 diterima (H0: β1 = β2 = β3)
Kesimpulan: Tidak ada perbedaan rata-rata penurunan berat badan yang signifikan dalam kategori metode diet
Demikianlah tadi ulasan penggunaan rumus dan tabel ANOVA dua arah (Two Way ANOVA). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: 2 Macam Analisis Regresi Linear

Sungkem sama yg bikin materi. Mudah banget dipahami.