Diketahui:
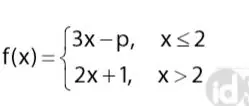
Agar limx → 2 f(x) mempunyai nilai maka nilai p = ….
Jawab:
Agar suatu titik mempunyai nilai limit maka nilai limit kiri (x mendekati 2 dari kiri: x → 2–) harus sama dengan limit kanan (x mendekati 2 dari kanan: x → 2+). Sehingga limx → 2 f(x) akan memiliki nilai saat memenuhi persamaan limx → 2– 3x − p = limx → 2+ 2x + 1.
Menentukan nilai a:
limx → 2– 3x − p = limx → 2+ (x + 1)
3(2) − p = 2 + 1
6 − p = 3
p = 6 − 3 = 3
Jadi, agar limx → 2 f(x) mempunyai nilai, maka nilai p = 3.