Apakah fungsi f(x) = x^3 + bx + c memotong sumbu-x di tepat satu titik?

Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.  

(1)  b > 0

(2)  bc > 0

(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

(B) Pertnyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

(C) DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup

(D) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.

(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Jawab: (A)

Fungsi f(x) = px³ + qx² + rx + s akan memotong sumbu x tepat pada satu titik saat memiliki satu buah titik stasioner. Misalnya pada fungsi f(x) = x³ yang memiliki satu titik stasioner yaitu pada titik (0, 0).

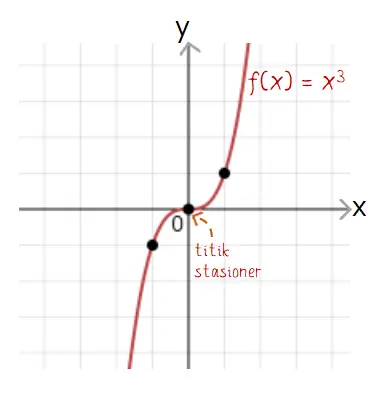
Titik stasioner dapat diketahui melalui nilai turunan pertama fungsi f(x) sama dengan nol, f'(x) = 0.

Turunan pertama fungsi f(x) = x³ + bx + c:

f'(x) = 3x² + b

Apakah fungsi f(x) = x^3 + bx + c memotong sumbu-x di tepat satu titik dapat diketahui nilai b yang memenuhi persamaan f'(x) = 3x² + b = 0.

Untuk pernyataan (1) b > 0:
Saat nilai b > 0 maka akan selalu menghasilkan nilai f'(x) > 0 karena 3x² akan selalu menghasilkan bilangan positif dan b > 0 selalu berupa bilangan positif.

Jumlah dari dua bilangan positif akan selalu berupa bilangan positif. Sehingga nilai f'(x) = 3x² + b akan selalu lebih dari nol. Dari pernyataan ini dapat digunakan untuk menjawab pertanyaan yang diberikan.

Untuk pernyataan (2)  bc > 0:
Nilai b dapat berupa bilangan posifif (b > 0) atau (b < 0) bergantung dari nilai c nya. Ada dua kemungkinan nilai b sehingga tidak cukup untuk memutuskan apa jawaban dari pertanyaan: Apakah fungsi f(x) = x^3 + bx + c memotong sumbu-x di tepat satu titik?

Kesimpulan: (A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.