Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a ‒ b adalah ….
A. 15
B. 11
C. 7
D. 4
E. 2
Jawab: D
Dari contoh soal transformasi geometri di atas dapat diperoleh beberapa informasi seperti berikut.
- Titik pusat dilatasi: (3, 1)
- Faktor skala dilatasi: k = 3
- Titik awal yang dipetakan: (5, b)
- Titik hasil dilatasi: (a, 10)
Persamaan untuk titik yang dipetakan dan hasil dilatasi suatu titik memenuhi bentuk umum rumus dilatasi berikut.
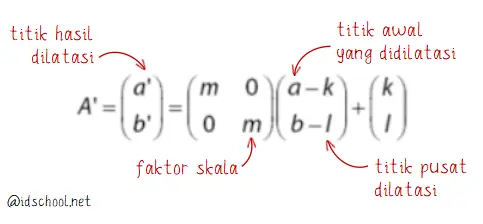
Sehingga bentuk persamaan untuk titik-titik dalam matriks transformasi dilatasi sesuai dengan bentuk berikut.
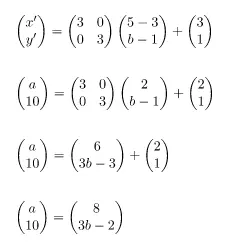
Diperoleh nilai a = 8,
selain itu diperoleh juga persamaan 3b ‒ 2 = 10 yang dapat digunakan untuk mendapatkan nilai b.
Mencari nilai b:
3b ‒ 2 = 10
3b = 10 + 2
3b = 12
b = 12/3 = 4
Menghitung nilai a ‒ b:
a ‒ b = 8 ‒ 4
a ‒ b = 4
Jadi, hasil akhir penyelesaian contoh soal transformasi geometri di atas adalah a ‒ b = 4.