Diketahui barisan dengan suku pertama U1 = 15 dan memenuhi Un − Un−1 = 2n + 3, n ≥ 2. Nilai U50 + U2 adalah ….

Diketahui barisan dengan suku pertama U1 = 15 dan memenuhi U_n − U_n−1 = 2n + 3, n ≥ 2. Nilai U₅₀ + U₂ adalah ….
(A)   2.688
(B)   2.710
(C)   2.732
(D)   2.755
(E)   2.762

Jawab: (C)

Dari soal diketahui barisan dengan suku pertama U1 = 15 dan memenuhi U_n − U_n−1 = 2n + 3, n ≥ 2:

• Suku pertama barisan: U₁ = 15
• Pola barisan: U_n − U_n−1 = 2n + 3, n ≥ 2

Dari rumus pola Un pola bilangan dapat diketahui U₂, U₃, dan U_n lainnya seperti berikut.

• Untuk n = 2:
  U₂ − U₁ = 2(2) + 3
  U₂ − 15 = 7
  U₂ = 7 + 15 = 22

• Untuk n = 3:
  U₃ − U₂ = 2(3) + 3
  U₂ − 22 = 9
  U₂ = 9 + 22 = 31

• Untuk n = 4:
  U₄ − U₃ = 2(4) + 3
  U₄ − 31 = 11
  U₄ = 11 + 31 = 42

• Untuk n = 50:
  U₅₀ − U₄₉ = 2(50) + 3
  U₅₀ − U₄₉ = 103
  U₅₀ = 103 + U₄₉

Sehingga untuk diketahui barisan dengan suku pertama U₁ = 15 dan memenuhi U_n − U_n−1 = 2n + 3 akan membentuk pola bilangan barisan berikut.

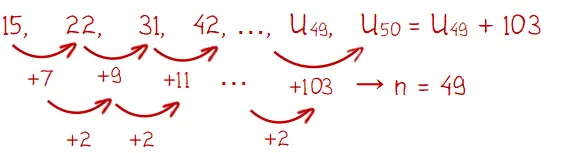
Sehingga,

U₅₀ = 15 + 7 + 9 + 11 + … + 103

U₅₀ = 15 + (7 + 9 + 11 + … + 103)

U₅₀ = 15 + 2.695 = 2.710

Diperolah nilai U₅₀ = 2.710 dan U₂ = 22. Jadi, nilai U₅₀ + U₂ = 2.710 + 22 = 2.732 (C).