Diketahui dua buah lingkaran dengan pusat A dan B, dengan panjang jari-jari masing-masing 7 cm dan 2 cm.

Diketahui dua buah lingkaran dengan pusat A dan B, dengan panjang jari-jari masing-masing 7 cm dan 2 cm. Jika jarak AB = 13 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah ….
A. 5 cm
B. 6 cm
C. 12 cm
D. 15 cm

Jawab: B

Rumus garis singgung persekutuan luar (d) 2 lingkaran:

d² = J² − (R − r)²

Keterangan:
d = garis singgung persekutuan luar
J = jarak kedua pusat lingkaran
R = jari-jari lingkaran besar
r = jari-jari lingkaran kecil

Berdasarkan keterangan pada soal diperoleh informasi berikut.

• Titik pusat lingkaran adalah A dan B
• Panjang jari-jari lingkaran besar: R = 7 cm
• Panjang jari-jari lingkaran kecil: r = 2 cm
• Jarak kedua pusat lingkaran: AB = 13 cm

Gambaran garis singgung persekutuan luar dua lingkaran beserta ukurannya terdapat pada bentuk berikut.

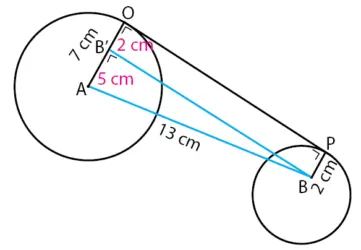
Menghitung panjang garis singgung persekutuan luar:
OP² = AB² − (R − r)²
OP² = 13² − (7 − 2)²
OP² = 13² − 5²
OP² = 169 − 25 = 144
OP = √144 = 12 cm

Jadi, panjang garis persekutuan luar kedua lingkaran tersebut saat diketahui dua buah lingkaran dengan pusat A dan B, panjang jari-jari masing-masing 7 cm dan 2 cm, serta jarak AB = 13 cm adalah OP = 12 cm.