Diketahui sistem persamaan 3x + 7y = 1 dan 2x – 3y = 16. Nilai xy = ….
A. 8
B. 6
C. –10
D. –12
Jawab: C
Nilai x dan y dari Sistem Persalaam Linear Dua Variabel (SPLDV) 3x + 7y = 1 dan 2x – 3y = 16 dapat diselesaikan dengan metode eliminasi, substitusi, atau campuran. Cara yang cukup ringkas dilakukan adalah metode campuran.
Pada metode campuran, langkah pertama dilakukan untuk menentukan nilai salah satu variabel. Langkah selanjutnya, nilai variabel yang diperoleh digunakan untuk metode substitusi.
Metode campuran untuk menyelesaikan sistem persamaan 3x + 7y = 1 dan 2x – 3y = 16 dilakukan seperti penyelesaian berikut.
Mencari nilai y dengan metode eliminasi:
Eliminasi x dari sistem persamaan 3x + 7y = 1 dan 2x – 3y = 16 untuk mendapatkan nilai y.
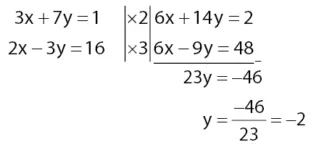
Mencari nilai x dengan metode substitusi:
Carabta substitusi nilai y = -2 pada persamaan 2x – 3y = 16 (atau 3x + 7y = 1, pilih salah satu)
2x – 3(-2) = 16
2x + 6 = 16
2x = 16 – 6 = 10
x = 10/2 = 5
Diperoleh nilai x = 5 dan y = ‒2 dari soal dengan diketahui sistem persamaan 3x + 7y = 1 dan 2x – 3y = 16. Nilai xy = 5 × (‒2) = ‒10.