Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem persamaan adalah himpunan persamaan yang saling berhubungan. Persamaan linear adalah persamaan yang memuat variabel dengan pangkat tertinggi sama dengan satu. Persamaan linear dua varibel berarti persamaan yang memuat dua varibel dengan pangkar tertinggi 1. Sehingga sistem persamaan linear dua variabel dapat dipahami sebagai himpunan persamaan-persamaan linear yang memiliki dua variabel. Penyebutan nama sistem persamaan linear dua variabel sering disingkat dengan SPLDV.

Sebuah persamaan linear memiliki komponen yang meliputi variabel, koefisien, dan konstanta. Koefisien dan variabel terletak berdampingan dengan letak koefisien di depan variabel. Konstanta pada persamaan linear adalah bilangan yang tidak diikuti oleh variabel. Contoh persamaan linear dua variabel adalah 3x + 2y = 12.

Bentuk Persamaan Linear

Persamaan linear dua variabel memiliki karakteristik memiliki sebagai persamaan dengan pangkat tertinggi dari semua variabel dalam persamaan adalah satu. Perhatikan persamaan yang bukan SPLDV dan persamaan yang merupakan SPLDV berikut.

Contoh bukan SPLDV:
2x² + 5x = 14
¹/_x + ¹/_y = 2

Contoh SPLDV:
2x + 5y = 14
3a + 4b =24
q + r = 3

Bentuk umum sistem persamaan linear dua variabel (SPLDV):
ax + by = c
dx + ey = f
Hasil penyelesaian SPLDV dinyatakan dalam pasangan terurut (x, y)

Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel

Terdapat beberapa cara/metode untuk menyelesaikan permasalahan terkait Sistem Persamaan Linear Dua Variabel (SPLDV). Empat metode yang dapat digunakan untuk menyelesaikan SPLDV adalah sebagai berikut.

Substitusi
Eliminasi
Gabungan
Grafik

Melalui halaman ini, sobat idschool dapat mengetahui proses pengerjaan SPLDV dengan berbagai metode. Untuk mengetahui perbedaan setiap metode, akan disajikan dalam pengerjaan sebuah soal dengan keempat metode tersebut.

Permasalahan dalam SPLDV yang akan diselesaikan adalah dua bersamaan berikut.
(i) 2x + 3y = 8
(ii) 3x + y = 5

Metode Substitusi

Ada beberapa langkah yang perlu dilakukan untuk menyelesaikan SPLDV dengan metode substitusi. Berikut ini adalah langkah-langkah menyelesaikan SPLDV dengan metode substitusi.

Langkah-langkah menyelesaikan SPLDV dengan metode substitusi:

Mengubah salah satu persamaan menjadi bentuk y = ax + b atau x = cy + d [TRIK!! Pilih persamaan yang paling mudah untuk diubah]
Substitusi nilai x atau y yang diperoleh pada langkah pertama ke persamaan yang lainnya
Selesaikan persamaan untuk mendapatkan nilai x atau y
Substitusi nilai x atau y yang diperoleh pada langkah ketiga pada salah satu persamaan untuk mendapatkan nilai dari variabel yang belum diketahui. Penyelesaiannya adalah (x, y)

Penyelesaian permasalahan SPLDV dengan metode substitusi:

Langkah 1: mengubah salah satu persamaan menjadi bentuk y = ax + b atau x = cy + d
Mengubah persamaan (ii) ke dalam bentuk y = ax + b
3x + y = 5 → y = 5 ‒ 3x

Langkah 2: substitusi y = 5 ‒ 3x pada persamaan 2x + 3y = 8
2x + 3(5 ‒ 3x) = 8

Langkah 3: selesaikan persamaan sehingga diperoleh nilai x
2x + 3(5 ‒ 3x) = 8
2x + 15 ‒ 9x = 8
‒7x = ‒7
x = 1

Langkah 4: substitusi nilai x = 1 pada persamaan 2x + 3y = 8 (pilih salah satu, hasilnya akan sama)
2x + 3y = 8
2(1) + 3y = 8
3y = 8 ‒ 2
3y = 6 → y = 2

Langkah 5:
Diperoleh penyelesaian dari sistem persamaan linear dua varibael dalam bentuk adalah (x, y). Hasil yang diperoleh adalah x = 1 dan y = 2, jadi penyelesaiannya SPLDV pada soal yang diberikan dalah (1, 2)

Baca Juga: Kumpulan Soal UN SMP – SPLDV

Metode Eliminasi

Cara kedua untuk menyelesaikan SPLDV adalah menggunakan metode eliminasi. Secara ringkas, dalam metode eliminasi adalah menghilangkan salah satu variabel untuk mendapatkan nilai dari satu variabel lainnya.

Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:

Menyamakan salah satu koefisien dari variabel x atau y dari kedua persamaan dengan cara mengalikan konstanta yang sesuai.
Hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan.
Ulangi kedua langkah untuk mendapatkan variabel yang belum diketahui.
Penyelesaiannya adalah (x, y)

Penyelesaian permasalahan dengan metode eliminasi diberikan seperti langkah-langkah di bawah.

Langkah 1: menyamakan salah satu koefisien dari variabel x atau y dari kedua persamaan dengan cara mengalikan konstanta yang sesuai.

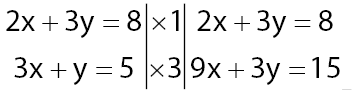
Langkah 2: hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan.

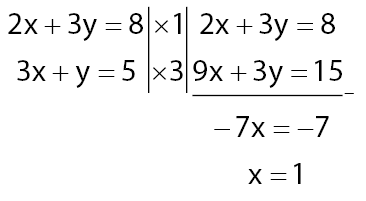
Langkah 3: ulangi kedua langkah untuk mendapatkan variabel yang belum diketahui

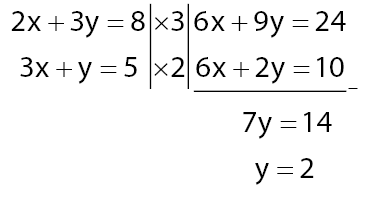
Langkah 4: penyelesaiannya adalah (x, y) → Hasil yang diperoleh x = 1 dan y = 2, jadi penyelesaiannya adalah (1, 2).

Cara Gabungan (Eliminasi-Substitusi) untuk Menyelesaikan Sistem Persamaan Linear 2 Variabel

Metode gabungan merupakan penggabungan langkah dari metode substitusi dan eliminasi. Metode eliminasi mempunyai langkah awal yang cukup mudah dan singkat. Sedangkan metode substitusi mempunyai cara akhir yang baik. Kedua metode tersebut digabungkan untuk mempermudah pengerjaan.

Metode gabungan merupakan metode yang sering digunakan dalam menyelesaikan SPLDV karena dinilai lebih ringkas dan baik.

Langkah-langkah menyelesaikan SPLDV dengan metode gabungan:

Cari nilai salah satu variabel x atau y dengan metode eliminasi
Gunakan metode substitusi untuk mendapatkan nilai variabel kedua yang belum diketahui
Penyelesaian sistem persamaan linear dua varibel berupa bentuk (x, y)

Contoh penyelesaian permasalahan SPLDV dengan metode gabungan (eliminasi – substitusi):

Langkah 1: mencari nilai x dengan metode eliminasi

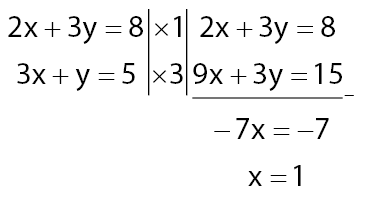
Sistem Persamaan Linear Dua Variabel (SPLDV))

Langkah 2: substitusi nilai x = 1 pada persamaan 2x + 3y = 8 (pilih salah satu, hasilnya akan sama)
2x + 3y = 8
2(1) + 3y = 8
3y = 8 ‒ 2
3y = 6
y = ⁶/₃ = 2

Langkah 3: penyelesaiannya adalah (x, y) → Hasil yang diperoleh x = 1 dan y = 2, jadi penyelesaiannya adalah (1, 2).

Metode Grafik

Penyelesaian SPLDV dengan metode grafik dilakukan dengan menentukan koordinat titik potong dari kedua garis yang mewakili kedua persamaan linear. Sebelumnya, sobat idschool perlu belajar mengenai cara menggambar garis pada persamaan linear terlebih dahulu.

Langkah-langkah menyelesaikan SPLDV dengan metode grafik:

Menggambar garis yang mewakili kedua persamaan dalam bidang kartesius
Menemukan titik potong dari kedua grafik tersebut
Penyelesaiannya adalah (x, y).

Berikut ini penyelesaian SPLDV dengan metode grafik.

Langkah 1: menggambar kedua grafik

Menentukan titik potong pada kedua sumbu x dan y dari kedua persamaan.

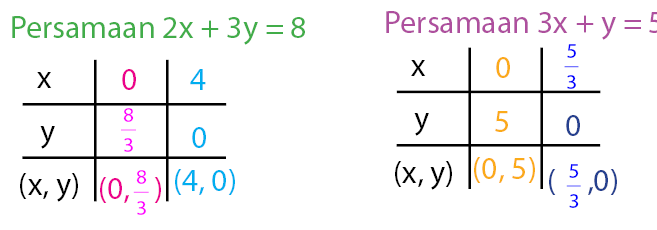
Gambar garis lurus untuk kedua persamaan linear dalam bidang kartesius diberikan seperti gambar di bawah.

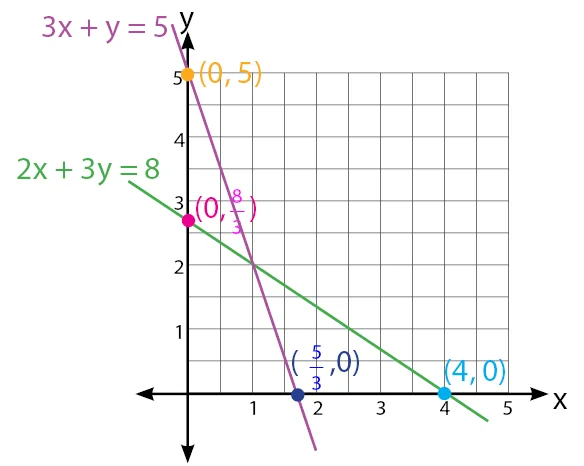
Menyelesaikan SPLDV dengan Metode Grafik

Langkah 2: menemukan titik potong dari kedua grafik tersebut.

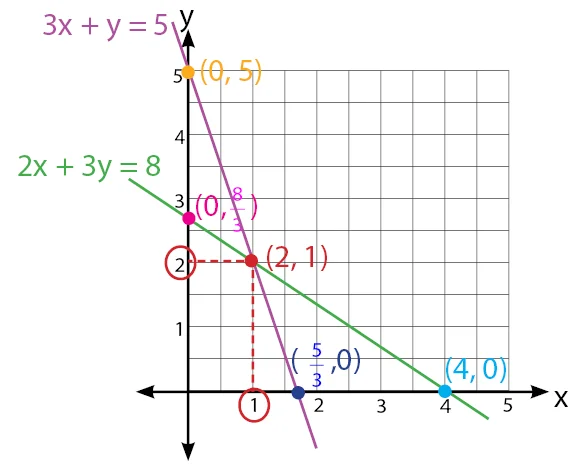
Langkah 3: penyelesaiannya adalah (x, y)

Berdasarkan gambar dapat diketahui bahwa titik potong berada pada x = 1 dan y = 2, jadi penyelesaiannya adalah (1, 2).

Dengan metode grafik, diperoleh pula hasil yang sama dengan metode substitusi, metode eliminasi, dan metode gabungan (substitusi – eliminasi).

Contoh Soal SPLDV dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Certia yang Sesuai dengan Sistem Persamaan Linear Dua Variabel

Diketahui sistem persamaan 3x + 2y = 8 dan x ‒ 5y = ‒37. Nilai 6x + 4y adalah ….
A. ‒30
B. ‒16
C. 16
D. 30

Pembahasan:

Dari persamaan x ‒ 5y = ‒37 dapat diperoleh persamaan yang ekuivalen yaitu x = 5y ‒ 37. Substitusi persamaan x ke dalam persamaan 3x + 2y = 8 untuk mendapatkan nilai y.

3(5y ‒ 37) + 2y = 8
15y ‒ 111 + 2y = 8
17y = 8 + 111
y = 119 : 17
y = 7

Selanjutnya, substitusi nilai y = 7 pada persamaan x = 5y ‒ 37 untuk mendapatkan nilai x.

x = 5y ‒ 37
x = 5×7 ‒ 37
= 35 ‒ 37
= ‒2

Jadi, nilai 6x + 4y = 6×(‒2) + 4×7 = ‒12 + 28 = 16

Jawaban: C

Contoh 2 – Soal Sistem Persamaan Linear

Seorang tukang parkir mendapat uang sebesar Rp17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah mobil dan 2 buah motor ia mendapat Rp18.000,00. Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang ia peroleh adalah ….
A. Rp135.000,00
B. Rp115.000,00
C. Rp110.000,00
D. Rp100.000,00

Pembahasan:

Misalkan:

Tarif parkir per mobil = x
Tarif parkir per motor = y

Berdasarkan cerita pada soal, dapat diperoleh model matematika seperti di bawah.

3x + 5y = 17.000
4x + 2y = 18.000

Kalikan persamaan pertama dengan 4 (empat) dan persamaan kedua dengan 3 (tiga). Hal ini digunakan untuk membuat salah satu variabelnya sama, sehingga bisa saling mengurangi.

Berdasarkan perhitungan di atas, diperoleh nilai y = 1.000

Substitusi nilai y = 1.000 pada salah satu persamaan yang diketahui, misalnya 3x + 5y =17.000 (pemilihan persamaan yang berbeda akan tetap menghasilkan hasil akhir sama).

3x + 5y = 17.000
3x + 5(1.000) = 17.000
x = (17.000 ‒ 5.000) : 3
x = 12.000 : 3 = 4.000

Hasil yang diperoleh adalah

Uang parkir mobil = x = Rp.4.000,00
Uang parkir motor = y = Rp.1.000,00

Jadi, uang yang diperoleh untuk 20 mobil dan 30 motor adalah
= 20 x Rp4.000,00 + 30 x Rp1.000,00
= Rp80.000,00 + Rp30.000,00 = Rp110.000,00

Jawaban: C

Demikianlah tadi ulasan materi sistem persamaan linear dua variabel atau yang sering disingkat sebagai SPLDV yang penyelesaiannya dapat dilakukan melalui metode substitusi, eliminasi, gabungan (eliminasi-substitusi), dan grafik. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Bava Juga: Sistem Persamaan Linear Tiga Variabel – SPLTV