Dua kapal A dan B meninggalkan pelabuhan P bersama-sama. Kapal A berlayar dengan arah ….

Dua kapal A dan B meninggalkan pelabuhan P bersama-sama. Kapal A berlayar dengan arah 30^o dan kecepatan 30 km/jam, sedangkan kapal B berlayar dengan arah 90^o dan kecepatan 45 km/jam.

Jika kedua kapal berlayar selama 2 jam, maka jarak kedua kapal tersebut adalah ….
A. 30√2 km
B. 30√5 km
C. 30√7 km
D. 30√10 km
E. 30√13 km

Jawab: C

Diketahui dua kapal A dan B meninggalkan pelabuhan P bersama-sama. Arah gerak kedua kapal tersebut sesuai dengan gambar berikut.

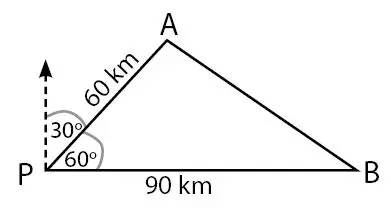
Jarak kedua kapal tersebut dapat dicari dengan aturan cosinus. Rumus aturan kosinus untuk menghitung panjang AB pada segitiga ABP di atas sesuai dengan persamaan berikut.

AB² = PA² + PB² − 2×PA×PB×cos ∠P

Menghitung panjang AB:
AB² = 60² + 90² − 2×60×90×cos 60^o
AB² = 3.600 + 8.100 − 2×60×90×¹/₂
AB² = 11.700 − 5.400 = 6.300
AB = √6.300 = √(900×7)
AB = √900 × √7 = 30√7 mil

Jadi, jarak terdekat dari pelabuhan A ke C adalah 30√7 mil.