Fitra membeli 3 buku dan 2 pensil seharga Rp11500,00. Prilly membeli 4 buku dan 3 pensil dengan harga Rp16.000,00. Jika Ika membeli 2 buku dan 1 pensil, jumlah uang yang harus dibayar adalah ….
A. Rp4.500,00
B. Rp6.500,00
C. Rp7.000,00
D. Rp7.500,00
Jawab: C
Misalkan:
x = harga buku
y = harga pensil
Membentuk persamaan matematis yang sesuai dengan soal cerita di atas.
- Fitra membeli 3 buku dan 2 pensil seharga Rp11500,00 → 3x + 2y = 11.500
- Prilly membeli 4 buku dan 3 pensil dengan harga Rp16.000,00 → 4x + 3y = 16.000
Diperoleh persamaan:
(i) 3x + 2y = 11.500
(ii) 4x + 3y = 16.000
Nilai x dan y dari sistem persamana linear dua variabel (SPLDV) di atas dapat lebih cepat diketahui dengan metode campuran.
- Pertama menentukan nilai x dengan metode elimnasi.
- Selanjutnya gunakan nilai x yang diperoleh untuk mencari nilai y dengan metode substitusi.
Menentukan nilai x:
Eliminasi y dari persamaan (i) dan (ii) untuk mendapatkan nilai x.
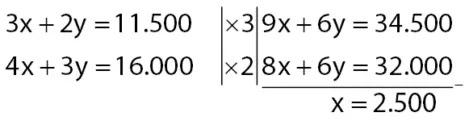
Substitusi nilai x = 2.500 pada persamaan 3x + 2y = 11.500 atau 4x + 3y = 16.000 (pilih salah satu, di sini akan menggunakan 3x + 2y = 11.500)
Menentukan nilai y:
3x + 2y = 11.500
3×2.500 + 2y = 11.500
7.500 + 2y = 11.500
2y = 11.500 ‒ 7.500 = 4.000
y = 4.000/2 = 2.000
Menghitung jumlah untuk membeli 2 buku dan 1 pensil:
= 2x + y
= 2×2.500 + 1×2.000
= 5.000 + 2.000 = 7.000
Jadi, harga 2 buku dan 1 pensil adalah Rp7.000,00