Jarak titik E ke bidang BDG adalah ….

Panjang rusuk ABCD.EFGH adalah 6 cm. Jarak titik E ke bidang BDG adalah ….
A. √3 cm
B. 2√3 cm
C. 3√3 cm
D. 4√3 cm
E. 6√3 cm

Jawab: D

Jarak titik ke bidang sama dengan panjang ruas garis terpendek yang menghubungkan titik dengan proyeksi titik tersebut pada bidang. Misalkan proyeksi titik E pada bidang BDG adalah titik P. Maka jarak titik E ke bidang BDG adalah panjang ruas garis EP.

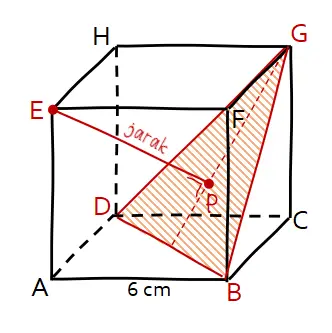
Panjang ruas garis EP dapat diketahui dengan dua cara yaitu cara cepat dan perhitungan panjang.

Cara I:

Untuk cara cepat, panjang ruas garis EP dapat dihitung dengan cara berikut.

Cara II:

Untuk perhitungan panjang, ada beberapa langkah perhitungan untuk mendapatkan panjang ruas garis EP. Bagaimana cara menghitung jarak P ke bidang BDG adalah menghitung panjang EP dari segitiga siku-siku PEG.

Namun sebelumnya perlu menghitung panjang EG dan PG terlebih dahulu.

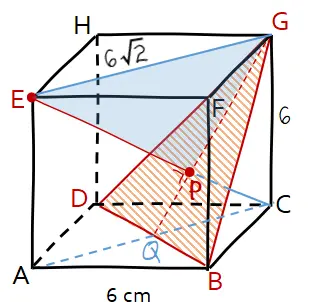
Ruas garis EG adalah diagonal sisi kubus, sehingga panjang EG = 6√2 cm. Sementara untuk mengetahui panjang ruas garis PG perlu mencari panjang CQ, GQ, dan PC terlebih dahulu.

1) Menghitung CQ:
CQ = ½ × diagonal sisi kubus
CQ = ½ × 6√2 = 3√2 cm

2) Menghitung GQ: (pandang ΔGCQ)
GQ² = GC² + CQ² = 6² + (3√2)²
GQ² = 36 + 18 = 54
GQ² = √54 = √(9×6) = 3√6 cm

3) Menghitung PC: (pandang ΔGCQ)
½×GQ×PC = ½×GC×CQ
3√6×PC = 6×3√2
√6×PC = 6√2

PC = √12 = √(4×3) = 2√3 cm

4) Menghitung PG: (pandang ΔGPC)
PG² = GC² − PC² = 6² − (2√3)²
PG² = 36 − 12 = 24
PG = √24 = (4×6) = 2√6 cm

Selanjutnya, panjang EG = 6√2 cm dan PG = 2√3 cm dapat digunakan untuk menghitung panjang EP seperti cara berikut.

Jadi, jarak titik E ke bidang BDG adalah 4√3 cm.