UTBK 2020/PK
Jika 4z = p dan p = 2q dengan p, q, z bilangan bulat positif manakah pernyataan di bawah ini yang benar?

(1)  z > p

(2)  q > z

(3)  z + q = p

(4)  q = 2z

(A)   (1), (2), dan (3) SAJA yang benar

(B)   (1) dan (3) SAJA yang benar

(C)   (2) dan (4) SAJA yang benar

(D)   HANYA (4) yang benar

(E)   SEMUA pilihan benar

Jawab: (C)

• Dari soal diketahui:
  • 4z = p
  • p = 2q

(1) z > p → SALAH karena z < p dengan alasan seperti penjelasan berikut.

Bukti:

4z = p = 2q

4z = 2q

z = ¹/₂q

Dari persamaan terakhir dapat disimpulkan bahwa nilai z sama dengan setengah q. Jadi, nilai z akan selalu kurang dari q (z < q) karena p, q, z bilangan bulat positif.

Dari persamaan p = 2q yang diketahui dapat disimpulkan bahwa nilai p sama dengan dua kali nilai q. Karena p, q, z adalah bilangan bulat positif, nilai p akan selalu lebih besar dari q (p > q).

Dengan demikian dapat diperoleh hubungan bilangan positif p, q, dan z  yaitu z < q < p.

(2)  q > z → BENAR kerena terdapat hubungan z < q < p sehingga nilai q > z.

(3)  z + q = p → SALAH karena z + q ≠ p, persamaan yang benar adalah 2z + q = p seperti yang ditunjukkan pada bukti berikut.

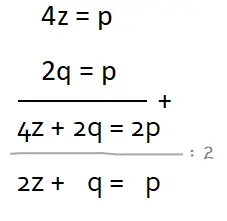
(4)  q = 2z → BENAR, buktinya terdapat pada proses perhitungan di bawah.

4z = p = 2q

4z = 2q

z = ¹/₂q

2z = q

Dari analisa yang dilakukan dapat diketahui bahwa pernyataan (1) dan (3) salah sementtara pernyataan (2) dan (4) benar.

Kesimpulan: (2) dan (4) SAJA yang benar