Jika K ⊂ L, L ⊂ M dan K′ adalah komplemen K, maka (M − L) ∪ (L − K)′ = ….
(A) M ∩ L′ ∩ K
(B) M ∩ (L ∪ K)
(C) M ∩ (L′ ∪ K′)
(D) L ∪ K′
(E) L′ ∪ K
Jawab: (E)
- Dari soal diketahui:
- K ⊂ L, L ⊂ M
- K′ = komplemen K
Dari keterangan yang diberikan dapat digambar diagram venn seperti berikut.
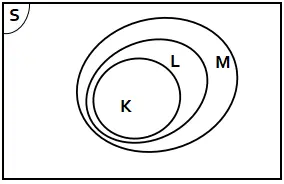
Sifat-sifat operasi himpunan:
- Kesamaan
- A ∪ A = A
- A ∩ A = A
- A – A = ∅
- Komutatif
- A ∪ B = B ∪ A
- A ∩ B = B ∩ A
- A + B = B + A
- Dalil De Morgan
- (A ∩ B)C = AC ∪ BC
- (A ∪ B)C = AC ∩ BC
- A – B = A ∩ BC
Sehingga,
(M − L) ∪ (L − K)′= (M ∩ L’)∪ (L ∩ K’)’
= M ∪(L’ ∪ (K’)’)
= M ∪(L’ ∪ K)
= (M ∪L’) ∪ K
= L’ ∪ K
Maka (M − L) ∪ (L − K)′= L′ ∪ K