UTBK 2022/PK
Jika kurva g(x) = 2 – x2 diperoleh dari menggeser kurva y = f(x) sejauh 3 satuan ke kanan dan 1 satuan ke atas, manakah pernyataan berikut yang benar?
(1) Kurva y = f(x) terbuka ke atas
(2) Garis y =1 menyinggung kurva y = f(x)
(3) Sumbu simetri kurva y = f(x) adalah x = 3
(4) f(x) < 0 untuk x > 0
(A) (1), (2), dan (3)
(B) (1) dan (3)
(C) (2) dan (4)
(D) (4)
(E) (1), (2), (3), dan (4)
Jawab: (C)
Pada pergeseran grafik berlaku ketentuan berikut:
- Jika grafik fungsi f(x) digeser secara horizontal (kanan-kiri) sejauh h satuan maka akan menjadi f(x+h).
- Untuk h > 0 → bergeser ke kiri
- Untuk h < 0 → bergeser ke kanan
- Jika grafik fungsi f(x) digeser secara vertikal (atas-bawah) sejauh h satuan maka akan menjadi f(x) + h.
- Untuk h > 0 → bergeser ke atas
- Untuk h < 0 → bergeser ke bawah
Dari soal diketahui bahwa g(x) diperoleh dari menggeser kurva y = f(x) sejauh 3 satuan ke kanan dan 1 satuan ke atas. Sehingga kurva f(x) adalah kurva g(x) = 2 – x2 yang digeser 3 satuan ke kiri dan 1 satuan ke bawah.
Menentukan persamaan f(x):
f(x) = g(x + 3) – 1
f(x) = 2 – (x + 3)2 – 1
f(x) = 2 – (x2 + 6x + 9) – 1
f(x) = –x2 – 6x – 9 + 2 – 1
f(x) = –x2 – 6x – 8
Gambar grafik fungsi kuadrat dengan persamaan f(x) = –x2 – 6x – 8:
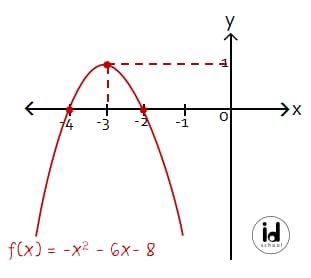
Perbandingan antara pernyataan yang diberikan dengan kondisi grafik sesungguhnya.
| Pernyataan | Kondisi sebenarnya |
| Kurva y = f(x) terbuka ke atas | Kurva y = f(x) terbuka ke bawah |
| Garis y =1 menyinggung kurva y = f(x) | Garis y = 1 menyinggung kurva y = f(x) |
| Sumbu simetri kurva y = f(x) adalah x = 3 | Sumbu simetri kurva y = f(x) adalah x = –3 |
| f(x) < 0 untuk x > 0 | f(x) < 0 untuk x > 0 |
Jadi, pernyataan berikut yang benar (2) Garis y =1 menyinggung kurva y = f(x) dan (4) f(x) < 0 untuk x > 0.