Jika luas permukaan bola 90 cm^2 maka luas seluruh permukaan tabung adalah ....

Perhatikan gambar di bawah!

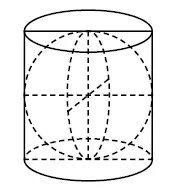
Jika luas permukaan bola 90 cm² maka luas seluruh permukaan tabung adalah ….
A. 160 cm²
B. 150 cm²
C. 135 cm²
D. 120 cm²

Jawab : C

Berdasarkan keterangan pada soal diketahui,

Luas permukaan bola: L_bola = 90 cm²
Bola menyinggung tutup, alas, dan selimut tabung sehingga:
*) Jari-jari tabung = jari-jari bola = r
*) Tinggi tabung: t_tabung = 2r

Penyelesaian soal membuthkan rumus luas permukaan bola dan tabung. Bentuk kedua rumus bangun terdapat pada persamaan berikut.

L_bola = 4πr²

Keterangan:
L_bola = luas permukaan bola (cm²)
r = jari-jari bola (cm)
π = 3,14159 atau π = ²²/₇

L_tab = 2πr×(r + t)

Keterangan:
L_tab = luas permukaan tabung (cm²)
r = jari-jari tabung (cm)
t = tinggi tabung (cm)
π = 3,14159 atau π = ²²/₇

Substitusi nilai luas bola yang diketahui untuk mendapatkan persamaan 2πr² yang dapat digunakan untuk menghitung luas tabung.

Menentukan persamaan 2πr² :
L_bola = 90
4πr² = 90
2πr² = ⁹⁰/₂ = 45

Menentukan luas tabung:
L_tabung= 2πr(r+t) = 2πr(r+2r)
L_tabung= 2πr² + 4πr² = 2πr² + 2(2πr²)
L_tabung = 45+2(45) = 45+90 = 135 cm²

Jadi, jika luas permukaan bola 90 cm² maka luas seluruh permukaan tabung adalah L_tabung = 135 cm².

Rumus Cepat!

Jika bola di dalam tabung menyinggung alas, tutup, dan selimut tabung maka berlaku L_tabung = ³/₂×L_bola.

Sehingga jika luas permukaan bola 90 cm² maka luas permukaan tabung dapat dihitung dengan cara berikut.

Menghitung luas tabung dengan cara cepat:
L_tabung = ³/₂×L_bola
L_tabung = ³/₂ × 90 = 135 cm²