Andi membeli 3 buku tulis, 1 bolpoint, dan 2 pensil dengan harga Rp17.000,00. Eci membeli 1 buku tulis, 2 bolpoint, dan 1 pensil dengan harga Rp13.000,00 sedangkan Eko membeli 2 buku tulis, 1 bolpoint, dan 1 pensil dengan harga Rp12.000,00. Merek barang tersebut sama.
Jika saya akan membeli 1 buku tulis dan 1 bolpoint maka harus membayar sebesar ….
A. Rp4.000,00
B. Rp5.000,00
C. Rp6.000,00
D. Rp7.000,00
E. Rp8.000,00
Jawab: D
Misalkan:
x = harga buku tulis
y = harga bolpoint
z = harga pensil
Menentukan persamaan yang sesuai dengan soal cerita:
- Andi membeli 3 buku tulis (3x), 1 bolpoint (y), dan 2 pensil (2z) dengan harga Rp17.000,00 → 3x+y+2z = 17.000
- Eci membeli 1 buku tulis (x), 2 bolpoint (2y), dan 1 pensil (z) dengan harga Rp13.000,00 → x+2y+z = 13.000
- Eko membeli 2 buku tulis (2x), 1 bolpoint (y), dan 1 pensil (z) dengan harga Rp12.000,00 → 2x+y+z = 12.000
Diperoleh tiga persamaan dengan 3 variabel:
(1) 3x + y + 2z = 17.000
(2) x + 2y + z = 13.000
(3) 2x + y + z = 12.000
Nilai x, y, dan z pada Sistem Persamaan Linear Tiga Variabel (SPLTV) di atas dapat lebih mudah dicari dengan metode campuran (eliminasi dan substitusi). Cara mendapatkan nilai x, y, dan z terdapat pada langkah penyelesaian berikut.
Berdasarkan persamaan (1) dan (2) akan diperoleh persamaan (4):

Berdasarkan persamaan (2) dan (3) akan diperoleh persamaan (5):

Eliminasi x dari persamaan (4) dan (5) untuk mendapatkan nilai x.
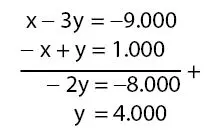
Substitusi nilai y = 4.000 pada persamaan (4) untuk mendapatkan nilai y:
x ‒ 3y = ‒9.000
x ‒ 3×4.000 = ‒9.000
x ‒ 12.000 = ‒9.000
x = ‒9.000 + 12.000 = 3.000
Diperoleh nilai x = 3.000 dan y = 4.000. Harga jika saya akan membeli 1 buku tulis dan 1 bolpoint sama dengan x + y = 3.000 + 4.000 = 7.000. Sehingga, jika saya akan membeli 1 buku tulis dan 1 bolpoint maka harus membayar sebesar Rp7.000,00.