SPLTV: Sistem Persamaan Linear Tiga Variabel

Sistem persamaan tiga variabel atau yang biasa disingkat sebagai SPLTV adalah kumpulan persamaan linear yang memiliki tiga variabel. Persamaan linear ditandai dengan pangkat tertinggi dari variabel dalam persamaan adalah satu. Selain itu, tanda yang menghubungkan persamaan berupa tanda sama dengan.

Dari bentuk umum tiga persamaan linear tiga variabel di atas, memuat tiga variabel yaitu variabel x, y, dan z. Dengan menyelesaikan tiga SPLTV akan diperoleh nilai variabel yang memenuhi semua persamaan linear yang terlibat dalam sistem.

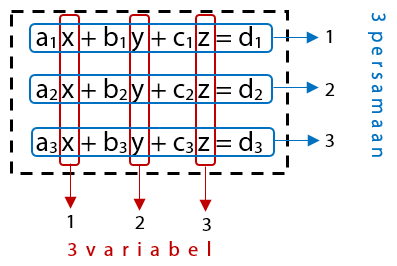
Bagaimana cara menyelesaikan soal sistem persamaan linear tiga variabel? Ada beberapa metode yang dapat sobat idschool perlu pelajari dan lakukan agar dapat menyelesaikan soal permasalahan yang melibatkan tiga variabel dan tiga persamaan. Metode tersebut diantaranya adalah susbtisusi, eliminasi, dan gabungan.

Bagaimana caranya? Simak penjelasan lebih lanjut pada masing – masing bahasan di bawah.

Table of Contents

• Menyelesaikan SPLTV dengan Metode Substitusi
• Menyelesaikan SPLTV dengan Metode Eliminasi
• Menyelesaikan SPLTV dengan Metode Gabungan (Eliminasi dan Substitusi)
• Contoh Soal SPLTV dan Pembahasannya

Menyelesaikan SPLTV dengan Metode Substitusi

Cara pertama yang dapat digunakan untuk menyelesaikan SPLTV adalah dengan metode substitusi. Proses pengerjaan SPLTV dengan metode substitusi dapat dilakukan dalam beberapa proses perhitungan.

Langkah pertama adalah mengubah persamaan menjadi satu persamaan yang ada pada sistem menjadi persamaan satu variabel atas dua variabel lainnya. Misalnya persamaan x dalam persamaan variabel y dan z, persamaan y dalam persamaan variabel x dan z, atau persamaan z dalam persamaan variabel x dan y.

Langkah kedua substitusikan fungsi persamaan satu variabel atas dua variabel lainnya ke dalam fungsi persamaan linear.

Berikutnya, lakukan perhitungan sampai diperoleh nilai x, y, dan z.

Contoh 1 – Menyelesaikan SPLTV dengan Metode Substitusi

Pembahasan:
Pertama, dari persamaan (i) x – 3y + z = 8 → x = 3y – z + 8 …. (iv), Substitusi persamaan (iv) ke persamaan (ii):
2x + 3y – z = 1
2(3y – z + 8) + 3y – z = 1
6y – 2z + 16 + 3y – z = 1
9y – 3z + 16 = 1
3z = 9y + 15
z = 3y + 5 …. (v)

Substitusi persamaan (iv) ke persamaan (iii):
3x – 2y – 2z = 7
3(3y – z + 8) – 2y – 2z = 7
9y – 3z + 24 – 2y – 2z = 7
7y – 5z + 24 = 7
5z = 7y + 24 – 7
5z = 7y + 17 …. (vi)

Substitusi persamaan (v) ke persamaan (vi):
5z = 7y + 17
5(3y + 5) = 7y + 17
15y + 25 = 7y + 17
15 y – 7y = -25 + 17
8y = -8 → y = – 1 …. (vii)

Substitusi nilai y = – 1 pada persamaan (vi) untuk mendapat nilai z.
5z = 7y + 17
5z = 7( – 1) + 17
5z = – 7 + 17
5z = 10 → z = 2 … (viii)

Substitusi nilai y = – 1 dan z = 2 pada persamaan (i) untuk mendapat nilai x.
x – 3y + z = 8
x – 3(- 1) + 2 = 8
x + 3 + 2 = 8
x + 5 = 8
x = 8 – 5 → x = 3

Diperoleh nilai ketiga variabel yang memenuhi sistem persamaan yaitu x = 3, y = – 1, dan z = 2. Sehingga, nilai x + y + z = 3 + (-1) + 2 = 4.

Jawaban: D

Mungkin langkah seperti di atas akan tidak sama dengan beberapa sobat idschool. Namun, jika perhitungan dilakukan dengan benar akan menghasilkan nilai yang sama.

Baca Juga: Kumpulan Soal UN untuk Materi SPLTV

Menyelesaikan SPLTV dengan Metode Eliminasi

Cara kedua untuk menyelesaikan permasalahan terkait sistem persamaan linear tiga variabel adalah metode eliminasi.

Metode eliminasi untuk menyelesaikan SPLTV dilakukan dengan mengeliminasi satu per satu variabel untuk mendapatkan nilai variabel lain dari dua persamaan yang berbeda. Dalam melakukan eliminasi variabel satu per satu, sobat idschool perlu melakukan kombinasi dua persamaan dari tiga persamaan yang diberikan.

Lakukan proses eliminasi satu per satu variabel sampai mendapatkan hasil semua variabel yang memenuhi persamaan dalam sistem.

Contoh 2 – Menyelesaikan SPLTV dengan Metode Eliminasi

Agar dapat membandingkan hasi yang diperoleh dari SPLTV, akan digunakan soal yang sama pada contoh 1 untuk diselesaikan dengan metode eliminasi.

Diberikan sistem persamaan linear tiga variabel:
(i) x – 3y + z = 8
(ii) 2x + 3y – z = 1
(iii) 3x – 2y – 2z = 7

Nilai x + y + z adalah ….
A. – 1
B. 2
C. 3
D. 4

Pembahasan:
Langkah pertama, eliminasi z dari persamaan (i) dan (ii):

Diperoleh nilai x = 3, selanjutnya, eliminasi x dari persamaan (i) dan (ii):

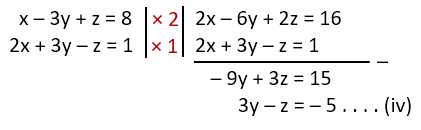
Eliminasi X dari persamaan (ii) dan (iii):

Eliminasi z dari persamaan (iv) dan (v) untuk mendapatkan nilai y:

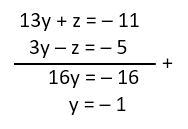
Eliminasi y dari persamaan (iv) dan (v) untuk mendapatkan nilai z:

Diperoleh nilai ketiga variabel yang memenuhi sistem persamaan yaitu x = 3, y = – 1, dan z = 2. Sehingga, nilai x + y + z = 3 + (-1) + 2 = 4.

Jawaban: D

Hasil yang sama dengan contoh 1 (soal yang sama), bukan?

Menyelesaikan SPLTV dengan Metode Gabungan (Eliminasi dan Substitusi)

Metode gabungan merupakan pengulangan dari kedua metode di atas (metode substitusi dan metode eliminasi). Pada metode gabungan, proses yang dilakukan memanfaatkan kelebihan dari masing – masing metode. Sehingga, cara menyelesaikan sistem persamaan linear tiga variabel dengan metode gabungan akan sobat idschool lebih sukai.

Simak cara menyelesaikan soal persamaan linear tiga variabel dengan metode gabungan berikut.

Contoh 3 – Cara Menyelesaikan SPLTV dengan Metode Gabungan

Diberikan sistem persamaan linear tiga variabel:
(i) x – 3y + z = 8
(ii) 2x + 3y – z = 1
(iii) 3x – 2y – 2z = 7

Nilai x + y + z adalah ….
A. – 1
B. 2
C. 3
D. 4

Pembahasan:
Untuk menyelesaikan sistem persamaan linear tiga variabel seperti yang diberikan pada soal, Pertama, eliminasi y dan z dari persamaan (i) dan (ii) untuk mendapatkan nilai x:

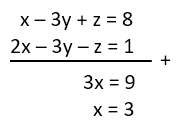
Selanjutnya, substitusi nilai x ke persamaan (i) untuk mendapatkan persamaan z dalam variabel x dan y.

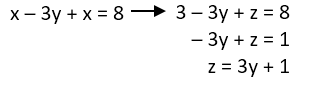
Substitusi x = 3 dan z pada persamaan (iv) ke persamaan (iii) untuk mendapatkan nilai y:
3x – 2y – 2z = 7
3 · 3 – 2y – 2(5 + 3y) = 7
9 – 2y – 10 – 6y = 7
–1 – 8y = 7
–8y = 8 → y = ⁸/_‒8 = ‒1

Selanjutnya, substitusi nilai x = 3 dan y = – 1 dari perhitungan di atas ke persamaan (i) untuk mendapatkan nilai z:
x – 3y + x = 8
3 ‒ 3(‒1) + z = 8
3 + 3 + z = 8
z = 8 – 6 → z = 2

Sehingga diperoleh hasil nilai variabel yang memenuhi ketiga sistem persamaan linear tiga variabel pada soal adalah x = 3, y = – 1, dan z = 2. Jadi nilai x + y + z = 3 + (– 1) + 2 = 4.

Jawaban: D

Soal yang sama dengan hasil akhir yang sama namun melalui cara yang berbeda, bukan? Untuk menambah pemahaman sobat idschool simak contoh – contoh soal SPLTV berikut.

Baca Juga: Sistem Persamaan Linear Dua Variabel – SPLDV

Contoh Soal SPLTV dan Pembahasannya

Pembahasan:
Langkah pertama buat pemisalan: p = ¹/_x; q = ¹/_y; dan r = ¹/_Z untuk memudahkan pengerjaan. Sehingga ketiga persamaan tersebut sesuai dengan persamaan-persamaan berikut.

Sehingga diperoleh persamaan baru yang ekuivalen dengan persamaan pada soal yang diberikan.

p + q + 3r = 9 _____(i)
p + 3q + r = ⁷/₃ ___(ii)
3p + q + r = 7 _____(iii)

Akan diselesaikan SPLTV seperti yang diberikan pada soal di atas dengan metode gabungan. Pertama, eliminasi p dari persamaan (i) dan (ii).

Selanjutnya eliminasi p dari persamaan (ii) dan (iii):

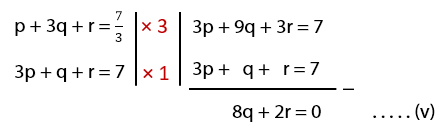
Untuk mendapatkan nilai q, eliminasi r dari persamaan (iv) dan (v):

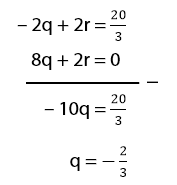
Substitusi q yang diperoleh hasil di atas pada persamaan (v) untuk mendapatkan nilai r.
8q + 2r = 0
8 · (‒²/₃)+ 2r = 0
‒¹⁶/₃ + 2r = 0
2r = ¹⁶/₃
r = ¹⁶/₃ : 2
r = ¹⁶/₃ × ¹/₂ = ⁸/₃

Berikutnya, substitusi nilai q dan r dari hasil perhitungan ke persamaan (i) untuk mendapatkan nilai p.
p + q + 3r = 9
p + (‒²/₃) + 3 × ⁸/₃ = 9
p ‒ ²/₃ + 8 = 9
p ‒ ²/₃ = 9 ‒ 8
p ‒ ²/₃ = 1
p = 1 + ²/₃ = ⁵/₃

Proses belum selesai sampai di sini, karena kita baru mendapatkan nilai p, q, dan r. Belum mendapatkan nilai x, y, dan z. Untuk mendapatkan nilai x, y, dan y kembali pemisalan yang dibuat di awal.

Demikianlah tadi ulasan materi cara menyelesaikan sistem persamaan tiga variabel (SPLTV). Cara yang dapat dilakukan meliputi metode eliminasi, metode substitusi, atau metode gabungan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Cara Menggambar Grafik Fungsi dari Persamaan Linear