Kamar Andi berbentuk balok dengan panjang 4 m, lebar 3 m, dan tinggi 3 m. Andi memasang lampu di tengah-tengah rusuk tegak salah satu pertemuan di dinding kamarnya.
Jarak sinar lampu terjauh di kamar Andi adalah ….
A. 1/2√109 m
B. 1/2√106 m
C. 1/2√91 m
D. 1/4√109 m
E. 1/2√106 m
Jawab: A
Misalkan setiap titik sudut kamar Andi berbentuk balok dengan panjang 4 m, lebar 3 m, dan tinggi 3 m diberi titik ABCD EFGH dan titik L berada di tengah-tengah garis AE.
Gambaran sinar lampu dalam kamar Andi nampak seberti berikut.
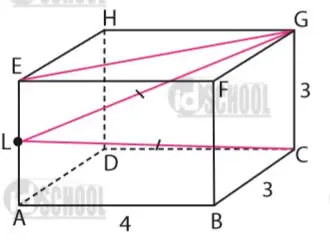
Jarak sinar lampu terjauh di kamar Andi adalah panjang ruas garis AG (sama dengan panjang ruas garis LC). Atau, jarak sinar lampu terjauh sama dengan jarak titik A ke titik G pada dimensi tiga.
Panjang ruas garis EG sama dengan panjang diagonal persegi panjang (p = EF = 4 m dan l = FG = 3 m).
Menghitung panjang EG:
EG2 = p2 + l2 = 42 + 32
EG2 = 16 + 9 = 25
EG2 = √25 = 5 m
Perhatikan bahwa segitiga GEL siku-siku di titik E. Panjang ruas garis LG dapat dihitung dengan rumus Pythagoras seperti langkah penyelesaian berikut.
Menghitung panjang LG:
LG2 = EG2 + EL2 = 52 + (3/2)2
LG2 = 25 + 9/4 = 100/4 + 9/4 = 109/4
LG = √109/4 = √109/√4 = 1/2√109 m
Jadi, jarak sinar lampu terjauh di kamar Andi berbentuk balok dengan panjang 4 m, lebar 3 m, dan tinggi 3 m adalah 1/2√109 m.