limx→−1
x2 − 2x − 3x2 − 1
= ….
A. 2
B. 1
C. 0
D. −1
E. −2
Jawab: A
Setiap kali mendapati soal limit, cek hasil substitusi nilai x yang mendekati fungsi. Untuk hasil substitusi nilai x yang mendekati pada soal lim x→-1 (x2 – 2x – 3)/(x2 – 1) = terdapat pada hasil dibawah.
limx→−1
x2 − 2x − 3x2 − 1
=
(−1)2 − 2(−1) − 3(−1)2 − 1
=
00
Dari hasil substitusi nilai x yang mendekati berupa bentuk tak tentu 0/0 sehingga Aturan L’ Hospital dapat digunakan. Selain menggunakan aturan tersebut, cara yang dapat juga digunakan adalah metode pemfaktoran.
Menentukan nilai limit limx→−1 (x2 – 2x – 3)/(x2 – 1) = dengan pemfaktoran:
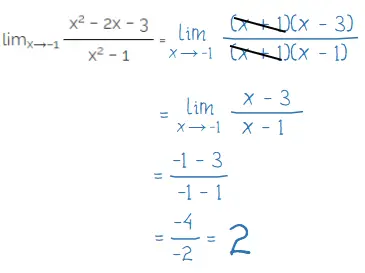
Jadi, lim x→-1 (x2 – 2x – 3)/(x2 – 1) = 2.