UTBK 2023
limx → 3
x – 3 3 – √(x + 6) = …
(A) –6
(B) –3
(C) 0
(D) 3
(E) 6
Jawab: (A)
Substitusi nilai x = 3 pada persamaan fungsi akan menghasilkan bentuk tak tentu 0/0. Sehingga nilai limit fungsi tersebut dapat dihitung dengan Aturan L’ Hospital.
Pertama, perlu mencari tahu turunan pertama fungsi pembilang f(x) = x − 3 dan fungsi penyebut g(x) = 3 − √(x+6) terlebih dahulu.
- f(x) = x − 3
f’(x) = 1
- g(x) = 3 − √(x+6)
g’(x) = −1/2√(x+6) → gunakan aturan rantai untuk mencari turinan fungsi
Menentukan nilai limit fungsi:
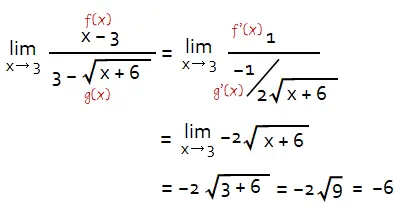
Jadi, lim x→3 x-3/3-√(x + 6) = −6