Limas segitiga beraturan T.ABC dengan panjang rusuk AB = 4 cm dan rusuk TA = 6 cm, maka jarak titik A ke garis TB adalah ….

Limas segitiga beraturan T.ABC dengan panjang rusuk AB = 4 cm dan rusuk TA = 6 cm, maka jarak titik A ke garis TB adalah ….

Jawab: E

Diketahui limas segitiga beraturan T.ABC dengan panjang rusuk AB = 4 cm dan rusuk TA = 6 cm. Ukuran dan bentuk limas T.ABC Berdasarkan keterangan pada soal terdapat pada gambar berikut.

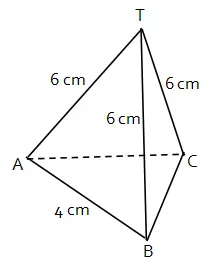
Misalkan titik O terletak pada ruas garis TB dan garis OA tegak lurus dengan garis TB. Jarak titik A ke titik TB sama dengan panjang ruas garis OA.

Untuk panjang BO = x cm, maka panjang TO = (6 − x) cm. Cara mencari panjang OA dapat menggunakan persamaan OA dari Teorema Pythagoras pada segitiga siku-siku AOB dan AOT.

Persamaan OA dari segitiga AOB:
OA² = AB² − OA²
OA² = 4² − x²
OA² = 16 − x²

Persamaan OC dari segitiga AOT:
OA² = AT² − OT²
OA² = 6² − (6 − x)²
OA² = 36 − (36 − 12x + x²)
OA² = 12x − x²

Menentukan nilai x:
16 − x² = 12x − x²
16 = 12x
x = ¹⁶/₁₂ = ⁴/₃ cm

Dari perhitungan diperoleh nilai x = ⁴/₃ cm. Substitusi nilai x pada salah satu persamaan OA untuk mendapatkan jarak titik A ke garis TB.

Menghitung jarak titik A ke garis TB:

Jadi, jarak titik A ke garis TB pada limas segitiga beraturan T.ABC dengan panjang rusuk AB = 4 cm dan rusuk TA = 6 cm adalah OA = ⁸/₃√2 cm.