Luas daerah tertutup yang dibatasi oleh parabola y = x2 dan y = 5x – 4 adalah … satuan luas.
A. 11/6
B. 8/3
C. 9/2
D. 11/2
E. 15/2
Jawab: C
Grafik parabola y = x2 berupa kurva mulus yang terbuka ke atas. Sementara y = 5x − 4 berupa garis lurus yang memotong sumbu x di titik (1, 0) dan memotong sumbu y di titik (0, −4).
Luas daerah tertutup yang dibatasi oleh parabola y = x2 dan y = 5x – 4 memiliki bentuk seperti gambar berikut.
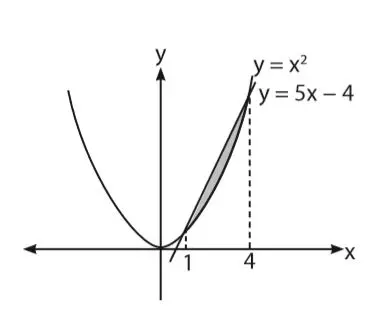
Dari grafik tersebut diketahui titik potong kurva dan garis adalah (1, 1) dan (4, 16). Dua nilai absis dari titik potong kurva dan garis menjadi batas integral pada perhitungan untuk menghitung luas.
Rumus intergal untuk menghitung luas daerah yang dibatasi 2 kurva:
L = a∫b (f(x2) − f(x1)) dx
Keterangan:
a dan b = batas integral
f(x1) dan f(x2) = persamaan kurva yang membatasi luas daerah
Pada soal diketahui persamaan f(x2) = y2 = x2 dan y f(x1) = y1 = 5x − 4. Batas integral perhitungan adalah a = 1 dan b = 4.
Menghitung luas daerah tertutup:
L = 1∫4 (5x − 4 − x2) dx
= [−1/3x3 + 5/2x2 − 4x]14
= [−1/3(4)3 + 5/2(4)2 − 4(4)] − [−1/3(1)3 + 5/2(1)2 − 4(1)]
= [−64/3 + 80/2 − 16] − [−1/3 + 5/2 − 4]
= −64/3 + 40 − 16 + 1/3 − 5/2 + 4
= 28 − 21 − 5/2
= 7 − 5/2 = 14/2 − 5/2 = 9/2
Jadi, luas daerah kurva yang dibatasi adalah L = 9/2 satuan luas.