Hasil integral suatu fungsi dapat diketahui melalui rumus integral. Bentuk rumus intergal tak tentu yang benar adalah ∫ f(x) dx = F(x) + C di mana f(x) adalah suatu fungsi dengan variabel x, F(x) adalah turunan pertama fungsi f(x). dan C adalah suatu konstanta. Sementara rumus integral tentu adalah a∫b f(x) dx = F(b) − F(a), dengan a dan b adalah batas atas dan bawah pengintegralan fungsi.
Fungsi f(x) dapat memiliki bentuk yang beragam, ada beberapa rumus integral yang bisa digunakan. Rumus umum integral bentuk dasar yang akan sering digunakan adalah ʃ xn dx = 1/n+1 xn+1 + C. Misalnya pada fungsi f(x) = 3x2 maka hasil integral fungsi f(x) adalah ʃ 3x2 dx = 3/2+1 x2+1 + C = 3/3 x3 + C = x3 + C.

Selain rumus dasar ʃ xn dx = 1/n+1 xn+1 + C, ada cukup banyak rumus integral lain yang dapat digunakan untuk menentukan hasil integral untuk berbagai bentuk fungsi f(x). Di mana rumus integral dapat dikelompokkan berdasarkan bentuk fungsinya yaitu fungsi rasional, irasional, trigonometri, eksponensial, dan logaritma.
Bagaimana saja bentuk rumus integral yang bisa digunakan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar Isi:
Rumus Integral
Rumus integral meliputi dua kelompok yaitu integral untuk fungsi dasar f(x) dan rumus integral parsial. Apa saja rumus yang berlaku terdapat pada daftar berikut.
1) Fungsi Dasar
Rumus integral bentuk dasar memuat beberapa teorema yang menyatakan persamaan hasil integral suatu fungsi. Bentuk dasar dari rumus integral dalam teorema-teorema tersebut digunakan untuk mempermudah dalam menentukan hasil integral suatu fungsi
Tujuh teorema yang menjadi rumus integral bentuk dasar terdapat pada persamaan-persamaan di bawah.
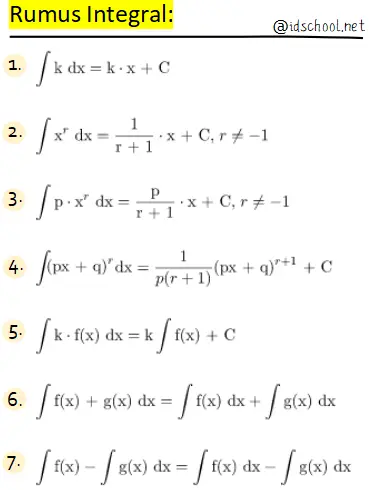
Setiap teorema selalu bisa dibuktikan, begitu juga untuk teorema mengenai rumus integral di atas. Pembuktian teorema fungsi integral cukup panjang dan tidak akan disertakan pada pemabahasan ini. Bagaimana pembuktian teorema tersebut dapat dilihat pada halaman pembuktian rumus integral.
2) Integral Parsial
Selain rumus integral untuk fungsi umum, ada rumus integral lain yang dapat digunakan untuk menentukan hasil integral suatu fungsi f(x) dengan ketentuan khusus yaitu rumus integral parsial. Penggunaan rumus ini biasanya untuk menentukan hasil integral dari fungsi f(x) dengan ketentuan berikut.
- Ada 2 fungsi yang dikalikan satu sama lain.
- Kedua fungsi memiliki derajat pangkat yang sama, salah satunya tidak bisa dijadikan turunan dari yang lain.
Beberapa fungsi f(x) hanya bisa ditentukan hasilnya dengan rumus integral parsial. Contoh fungsi yang hasilnya diperoleh menggunakan rumus integral adalah f(x) = ʃ 2x ex dx.
Rumus integral parsial adalah ʃ u dv = uv − ʃ v du.
Dalam menentukan hasil integral suatu fungsi f(x) dengan rumus integral parsial perlu tepat dalam menentukan fungsi mana yang menjadi u dan mana yang menjadi dv.
Tips untuk menentukan u dapat gunakan prinsip LIATE (log, invers, aljabar, trigonometri, dan eksponen).
Jika ada fungsi log, maka fungsi log itulah yang dijadikan sebagai u. Namun jika tak ada fungsi log maka fungsi invers yang jadi u. Kemudian seterusnya urutan fungsi mana yang menjadi u berikutnya adalah aljabar, trigonometri, dan eksponen.
Contoh penggunaan rumus integral parsial terdapat pada langkah penyelesaian untuk menentukan hasil integral fungsi f(x) = ʃ 2x ex dx berikut.

Baca Juga: Aplikasi Integral untuk Mencari Volume Benda Putar
Macam-Macam Rumus Integral
Rumus integral dapat dikelompokkan berdasarkan bentuk fungsinya yaitu fungsi rasional, irasional, trigonometri, eksponensial, dan logaritma. Berbagai macam rumus integral tersebut terdapat pada daftar berikut.
- Rumus integral fungsi rasioal:
- ∫ 1 dx = x + C
- ∫ a dx = ax+ C
- ∫ xn dx = 1/n+1xn+ 1 + C; n≠1
- Rumus integral fungsi irasional:
- Rumus intgral fungsi trigonometri:
- ∫ sin x dx = –cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ csc2x dx = –cot x + C
- ∫ sec x ∙ tan x dx = sec x + C
- ∫ csc x ∙ cot x dx = –csc x + C
- Rumus integral fungsi eksponensial:
- ∫ 1/x dx = ln |x| + C
- ∫ ex dx = ex + C
- ∫ ax dx = ax/ln a + C; a>0, a≠1
- Rumus integral fungsi logaritma:
Logaritma umum:
- ∫ alog x dx= x alog x − x/ln a + C
Logaritma natural (ln):
- ∫ ln x dx = x ln x − x + C
- ∫ ln ax dx = x ln ax − x + C
- ∫ (ln x)2 dx = x (ln x)2 − 2x ln x + 2x + C
Baca Juga: Rumus Integral Fungsi Trigonometri
Rumus Integral Tak Tentu dan Tentu
Bentuk fungsi integral terbagi menjadi dua jenis yaitu integral tak tentu dan integral tentu. Kedua bentuk integral terdapat pada ada/tidaknya batas pengintegralan.
Pada integral tak tentu, fungsi integral tidak memiliki batas integral. Sedangkan pada integral tentu, fungsi integral memiliki suatu rentang nilai yang menjadi batas integral.
1) Integral Tak Tentu
Integral tentu merupakan integral tanpa batas yang telah ditentukan. Bentuk umum integral tak tentu dinyatakan dalam bentuk berikut.
ʃ f(x) dx = F(x) + C
Aturan dasar menemukan nilai suatu integral ditunjukkan seperti persamaan di atas. Bagaimana cara menentukan hasil fungsi integral ditunjukkan dalam beberapa contoh berikut.
Contoh 1: ʃ 2x dx = . . .
ʃ 2x dx = 2/1+1 x1+1 + C
= 2/2 x2 + C
= x2 + C
Contoh 2: ʃ (x2 + 2x + 1) dx = . . .
ʃ(x2+2x+1) dx = ʃ x2 dx + ʃ 2x dx + ʃ 1 dx
= 1/2+1x2+1 + 2/1+2x1+1 + 1/0+1x0+1 + C
= 1/3x3 + 2/2x2 + 1/1x1 + C
= 1/3x3 + x2 + x + C
Contoh 3:
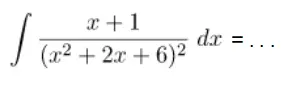
Cara menentukan hasil fungsi integral di atas dilakukan dengan pemisalan u = x2 + 2x + 6 sehingga du = (2x + 2) dx. Dengan pemisalan tersebut akan diperoleh fungsi f(u) yang lebih mudah ditentukan hasil integralnya seperti yang dilakukan pada langkah penyelesaian berikut.

Baca Juga: Pengertian Fungsi Turunan dan 8 Teoremanya
2) Integral Tentu
Integral tentu merupakan fungsi integral yang memiliki batas atas dan batas bawah pengintegralan. Bentuk umum integral tentu dinyatakan dalam persamaan berikut.
aʃb f(x) dx = F(b) ‒ f(a)
Integral tentu memiliki sifat-sifat yang dapat digunakan untuk mempermudah proses perhitungan integral. Beberapa sifat integral tentu terdapat pada daftar berikut.
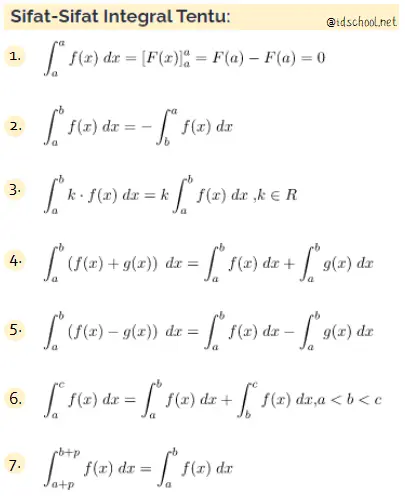
Cara menentukan hasil fungsi integral tentu tidak berbeda dari cara menentukan fungsi integral tak tentu. Hanya di akhir penyelesaian perlu dilakukan perhitungan tambahan. Di mana pada proses mencari nilai integral tentu dilakukan substitusi nilai yang menjadi batas pengintegralan fungsi.
Bagaimana cara menentukan nilai hasil fungsi integral tentu dilakukan seperti pada penyelesaian contoh 4 berikut.
Contoh 4: 1ʃ3 x3 √(x4 + 11) dx = ….
Langkah pengerjaan soal integral tentu sperti di atas dilakukan melalui pemisalan. Misalkan u = x4 + 11 maka du = 4x3 dx atau dx = du/4x3.
Dengan pemisalan yang dilakukan akan diperoleh fungsi yang lebih mudah untuk ditentukan hasil integralnya. Cara menentukan hasil fungsi integral pada contoh 4 dilakukan seperti tahap penyelesaian berikut.

Baca juga: Integral Substitusi dan Parsial
Contoh soal dan pembahasan
Beberapa contoh soal di bawah dapat sobat idshcool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Integral

Pembahasan:
Misalkan u = 3x2 + 9x ‒ 1 maka du = (6x + 9) dx atau du/dx = 6x + 9
Dengan pemisalan tersebut akan dipeorleh fungsi integral yang lebih mudah untuk diselesaikan. Cara menentukan hasil fungsi intergal tersebut terdapat pada langkah pengerjaan berikut.

Jadi, hasil fungsi integral tersebut adalah 2/3√(3x2 + 9x ‒ 1).
Jawaban: C
Baca Juga: Rumus Luas Daerah yang Dibatasi Kurva
Contoh 2 Soal Integral
Diketahui 1ʃt (3p ‒ 2)(4 + p) dp = 50. Nilai dari 3t adalah . . . .
A. 12
B. 9
C. 6
D. 3
E. 2
Pembahasan:
Langkah pertama yang perlu dilakukan adalah menentukan hasil fungsi integral tentu pada soal. Cara menentukan hasil fungsi integral fungsi tentu dapat dilakukan seperti cara berikut.

Dari hasil pengerjaan di atas diperoleh fungsi t dengan pangkat tertinggi 3 yaitu t3 + 5t2 ‒ 8t + 2 = 50. Untuk mendapatkan nilai t perlu dilakukan pemfaktoran polinomial seperti yang dilakukan pada cara berikut.
t3 + 5t2 ‒ 8t + 2 = 50
t3 + 5t2 ‒ 8t + 2 ‒ 50 = 0
t3 + 5t2 ‒ 8t + 48 = 0
(t ‒ 3)(t + 4)(t + 4) = 0
Dapat diperoleh nilai t yang memenuhi persamaan t3 + 5t2 ‒ 8t + 48 = 0 ada dua yaitu,
- t ‒ 3 = 0
t = 3
- t + 4 = 0
t = ‒4
Ada dua nilai t yang memenuhi nilai fungsi integral 1ʃt (3p ‒ 2)(4 + p) dp = 50 yaitu t = 3 atau t = ‒4. Sehingga ada dua nilai 3t yaitu 3t = 9 atau 3t = ‒12.
Pada pilihan ganda yang diberikan ada satu jawaban yang memenuhi yaitu 3t = 9. Jadi, nilai dari 3t adalah 9.
Jawaban: B
Sekian pembahasan mengenai rumus integral tak tentu untuk menentukan hasil fungsi integral f(x). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
