UTBK 2023

(A)   −2
(B)    0
(C)   2
(D)   6
(E)   8

Jawab: (C)

Setiap menjumpai soal limit, coba substitusi nilai x yang mendekati fungsi ke persamaannya. Untuk soal ini lakukan untuk nilai x = 3. Hasil substitusi x = 3 ke persamaan akan menghasilkan nilai bentuk tak tentu ⁰/₀ seperti hasil perhitungan berikut.

Tentu hasil akhir tersebut bukan nilai limitnya. Untuk setiap hasil substitusi berupa bentuk tak tentu ⁰/₀ atau ^∞/_∞, nilai limit fungsi dapat dicari tahu dengan Aturan L’ Hospital.

Cara I:

Cara menetukan nilai limit dengan Aturan L’ Hospital terdapat pada langkah penyelesaian berikut.

Cara II:

Selain dengan Aturan L’ Hospital, nilai limitnya dapat dicari menggunakan pemfaktoran. Caranya seperti yang dilakukan pada langkah penyelesaian berikut.

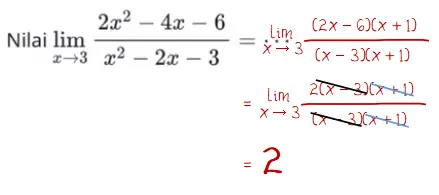
Jadi, nilai lim x→3 (2x^2 – 4x – 6)/(x^2 – 2x – 3) = 2.