Nilai lim x → 0 (2x Sin 3x)/(1 – Cos 6x) = . . . .

A. −1
B. −¹/₃
C. 0
D. ¹/₃
E. 1

Jawab: D

Substitusi nilai x pada persamaan ^{2x∙ sin 3x}/_{1 – Cos 6x} tidak menghasilkan bentuk tak tentu 0/0 atau ∞/∞. Sehingga Aturan L’ Hospital tidak bisa digunakan.

Cara menentukan nilai lim x → 0 ^{2x∙ sin 3x}/_{1 – Cos 6x} menggunakan identitas trigonometri dan bentuk dasar rumus limit fungsi trigonometri,

Identias tirogonmetri yang dibutuhkan untuk meneyelesaikan soal adalah cos 6x = 1 − 2 sin²3x. Sedangkan rumus limit fungsi trigonometri yang digunakan untuk mencari nilai limitnya adalah lim_{x → 0} ^ax/_{sin bx} = ^a/_b. Penggunaan kedua rumus terdapat pada langkah penyelesaian berikut.

Menentukan nilai limit fungsi:

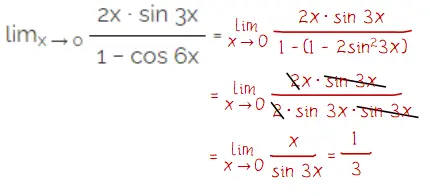
Jadi, nilai lim x → 0 (2x sin 3x)/(1 – cos 6x) = ¹/₃.