A. 3
B. 2½
C. 2
D. 1
E. −1
Substitusi nilai lim x → 1 ke persamaan x2 − 5x + 4/x3 − 1 akan menghasilkan bentuk tak tentu 0/0 seperti perhitungan berikut.
Hasil substitusi nilai menghasilkan bentuk tak tentu sehingga nilai limitnya dapat dicari dengan Dalil L’ Hospital. Di mana aturan tersebut hanya berlaku saat substitusi nilai x yang mendekati ke persamaan menghasilkan bentuk tak tentu 0/0 atau ∞/∞.
Dalil L’ Hospital:
Keterangan:
f'(x) = turunan pertama fungsi f(x)
g'(x) = turunan pertama fungsi g(x)
Pada soal terdapat fungsi f(x) = x2 − 5x + 4 fan g(x) x3 − 1. Sehingga turunan pertama kedua fungsi tersebut adalah f'(x) = 2x − 5 dan g'(x) = 3x2.
Menentukan limit dengan dalil L’ Hospital:
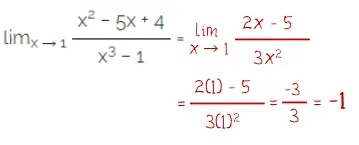
Cara lain untuk menentukan limit fungsi tersebut dapat dengan cara pemfaktoran aljabar seperti yang dilakukan pada langkah penyelesaian berikut.
Jadi, nilai lim x → 1 (x^2 − 5x + 4)/(x^3 − 1) = −1.