Pemfaktoran Bentuk Aljabar merupakan bagian dari operasi hitung bentuk Aljabar. Fungsi dari operasi pemfaktoran Aljabar adalah membuat suatu persamaan menjadi lebih sederhana. Bentuk sederhana dari suatu fungsi aljabar dapat memudahkan proses perhitungan.
Aljabar memuat bentuk persamaan yang memuat variabel, misalnya adalah 2x + 3y, 4m + 9n, dan lain sebagainya. Persamaan aljabar juga dapat berbentuk persamaan kuadrat seperti x2 + bx + c, atau dapat juga memiliki bentuk persamaan dengan variabel lebih tinggi. Cara menentukan persamaan bentuk aljabar cukup mudah dilakukan dengan beberapa cara, tergantung benntuk soal.
Apa saja bentuk persamaan dalam pemfaktoran bentuk Aljabar? Bagaimana cara melakukan operasi hitung pemfaktoran Aljabar? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Baca Juga: Operasi Hitung Aljabar
Operasi Hitung Pemfaktoran Aljabar dari Berbagai Bentuk
Soal dalam faktor aljabar sering disajikan dalam beberapa bentuk. Bentuk-bentuk faktor aljabar tersebut meliputi bentuk distributif, bentuk selisih kuadrat, bentuk kuadrat sempurna, bentuk x2 + bx + c = 0, dan bentuk ax2 + bx + c = 0 dengan nilai a ≠ 1.
Beberapa bentuk persamaan umum aljabar dan hasil faktornya dapat disimak seperti pada ulasan di bawah.
1. Bentuk Distributif:
Sifat distributif pada pemfaktoran bentuk Aljabar:
- px + py = p(x + y)
- px ‒ py = p(x ‒ y)
Contoh:
- 3x + 3y = 3(x + y)
- 5x ‒ 5y = 5(x ‒ y)
2. Bentuk Selisih Kuadrat:
Pemfaktoran selisih dari kuadrat dua bilangan: a2 ‒ b2 = (a + b)(a ‒ b)
Contoh: Tentukan faktor dari 9x2 ‒ 16!
Dari persamaan 9x2 ‒ 16 dapat diperoleh bahwa:
- a2 = 9x2 → a = 3x
- b2 = 16 → b = 4
Sehingga, 9x2 ‒ 16 = (3x)2 ‒ 42 = (3x + 4)(3x ‒ 4)
3. Bentuk Kuadrat Sempurna:
Pemfaktoran persamaan kuadrat sempurna:
- x2 + 2xy + y2 = (x + y)(x + y) = (x + y)2
- x2 ‒ 2xy + y2 = (x ‒ y)(x ‒ y) = (x ‒ y)2
Contoh:
- x2 + 6x + 9 = (x + 3)2
- x2 ‒ 6x + 9 = (x ‒ 3)2
4. Bentuk x2 + bx + c = 0:
Pemfaktoran pada bentuk umum persamaan kuadrat: x2 + bx +c = (x + p)(x+q) dengan nilai p + q = b dan p × q = c.
Contoh: Faktorkan bentuk x2 ‒ 7x + 12 = 0!
Berdasarkan persamaan kuadrat x2 ‒ 7x + 12 = 0 dapat diketahui bahwa nilai a = 1, b = ‒7, dan c = 12
Untuk mendapatkan faktor persamaan kuadrat x2 ‒ 7x + 12 = 0 dapat dilakukan melalui beberapa langkah berikut.
- Cari bilangan p dan q yang memenuhi
*Jika dikalikan hasilnya 12 → p × q = c = 12
*Jika dijumlahkan hasilnya ‒7 → p + q = b = ‒7
Tabel di bawah dapat digunakan untuk mempermudah dalam menentukan nilai p dan q.

Sehingga diperoleh nilai p dan q yang memenuhi adalah p = ‒4 dan q= ‒3 (nilai p dan q tertukar tidak akan menjadi masalah). Jadi, hasil pemfaktoran yang benar adalah x2 ‒ 7x + 12 = (x ‒ 4)(x ‒ 3).
5. Bentuk ax2 + bx + c = 0 dengan a ≠1
Pemfaktoran pada bentuk umum persamaan kuadrat dengan koefisien pangkat tertinggi a:
ax2 + bx +c = a( x +p/a)(x+q/a)
dengan nilai,
- p + q = b
- p × q = ac
Contoh: Faktorkan persamaan kuadrat 2x2 ‒ 11x + 15!
Penyelesaian pemfaktorannya untuk persaman kuadrat 2x2 ‒ 11x + 15 dapat dilihat seperti langkah-langkah di bawah.
- Dari persamaan kuadrat 2x2 ‒ 11x + 15 dapat diketahui bahwa nilai
a = 2
b = ‒11
c = 15
- Cari bilangan p dan q yang memenuhi persamaan dengan ketentukan seperto berikut.
*Jika dikalikan hasilnya sama dengan 30 → p × q = a × c = 2 × 15 = 30
*Jika dijumlahkan hasilnya sama dengan ‒11 → p + q = b = ‒11
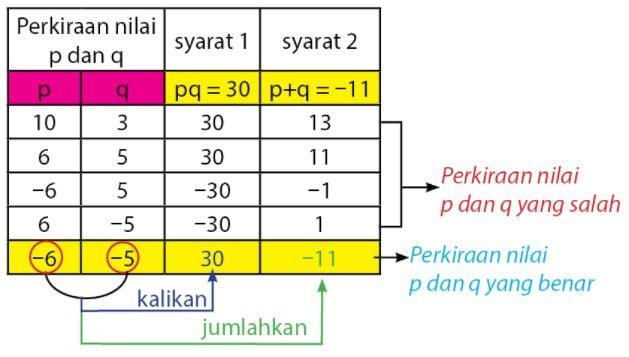
Perhatikan tabel di bawah untuk memudahkan bagaimana cara mendapatkan nilai p dan q yang memenuhi.
Diperoleh nilai p dan q yang memenuhi adalah p = ‒5 dan q = ‒6, sehingga pemfaktoran untuk persamaan kuadrat 2x2 ‒ 11x + 15 dapat diperoleh seperti cara berikut.
2x2 ‒ 11x + 15 = 2(x + (‒5/2))( x + (‒6/2))
= (2x + 2 × ‒5/2 )(x ‒ 3)
= (2x ‒ 5)(x ‒ 3)
Jadi hasil faktor untuk persamaan 2x2 ‒ 11x + 15 adalah (2x ‒ 5)(x ‒ 3).
Baca Juga: Operasi Hitung Bentuk Aljabar
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahamahan bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannnya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Pemfaktoran Bentuk Aljabar
Perhatikan pernyataan berikut!
I. 4x2‒9 = (2x+3)(2x‒3)
II. 2x2 + x ‒ 3 = (2x‒3)(x+1)
IIII. x2 + x ‒ 6 = (x+3)(x‒2)
IV. x2 + 4x ‒ 5 = (x‒5)(x+1)
Pernyataan yang benar adalah .…
A. I dan II
B. II dan III
C. I dan III
D. II dan IV
Pembahasan:
Selidiki pernyataan I:
Bentuk 4x2 ‒ 9 = (2x+3)(2x‒3) merupakan bentuk selisih kuadrat a2 ‒ b2 = (a‒b)(a+b) dengan a = 2x dan b=3. Sehingga,
4x2 ‒ 9 = (2x)2 ‒ 32
4x2 ‒ 9 = (2x+3)(2x‒3) → pernyataan I: Benar
Selidiki pernyataan II:
Bentuk 2x2 + x ‒ 3 merupakan bentuk ax2 + bx + c = 0 dengan a ≠ 1. Cara menentukan pemfaktoran persamaan tersebut diberikan seperti pada langkah berikut.
- Dari persamaan kuadrat 2x2 + x ‒ 3 dapat diketahui bahwa nilai a = 2, b = 1, dan c = ‒3
- Mencari bilangan p dan q yang memenuhi persamaan dengan ketentuan seperti berikut.
*p×q = a×c = 2 × ‒3 = ‒6
*p + q = b = 1
Nilai p dan q dapat diperoleh dengan cara seperti pada tabel di bawah.
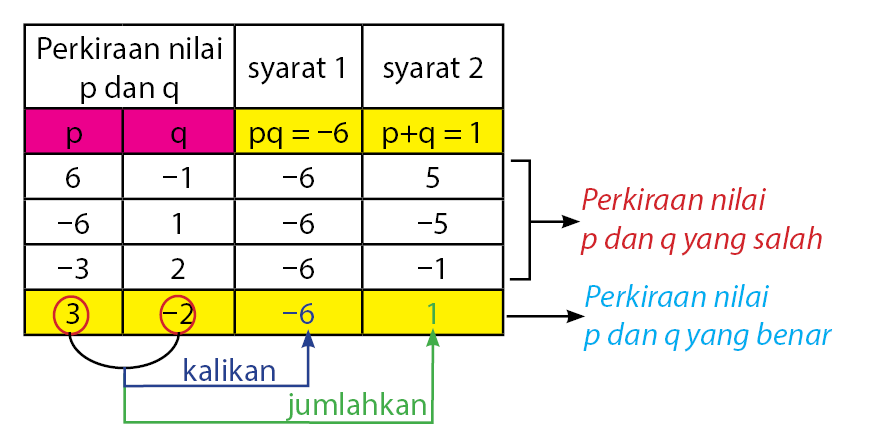
Sehingga diperoleh nilai p dan q yang memenuhi adalah p = 3 dan q = ‒2, maka hasil pemfaktoran persamaan tersebut adalah sebagai berikut.
2x2 + x ‒ 3 = 2( x + 3/2 )(x + ‒2/2)
= (2x + 2 × 3/2 )( x + ‒2/2)
= (2x + 3)(x ‒ 1)
Jadi 2x2 + x ‒ 3 ≠ (2x ‒ 3)(x+1), tetapi 2x2 + x ‒ 3 = (2x + 3)(x ‒ 1).
Selidiki pernyataan III:
Bentuk x2 + x ‒ 6 merupakan persamaan kuadrat dengan bentuk umum x2 + bx + c = 0.
Dari persamaan kuadrat x2 + x ‒ 6 dapat diketahui bahwa nilai a = 1, b = 1, dan c = ‒6.
Cara pemfaktorannya adalah sebagai berikut.
- Cari bilangan p dan q yang memenuhi persamaan di bawah:
p × q = c = ‒6
p + q = b = 1
Nilai p dan q yang memenuhi adalah p = 3 dan q = ‒2. Jadi, hasil pemfaktoran yang benar adalah x2 + x ‒ 6 = (x + 3)(x – 2).
Selidiki pernyataan IV:
Bentuk x2 + 4x ‒ 5 merupakan persamaan kuadrat dengan bentuk umum x2 + bx + c = 0. Dari persamaan kuadrat x2 + 4x ‒ 5 dapat diketahui bahwa nilai a = 1, b = 4 dan c = ‒5.
Cara pemfaktorannya adalah melalui beberapa langkah sebagai berikut.
Cari bilangan p dan q yang memenuhi persamaan berikut.
*p×q = c = ‒5
*p + q = b = 4
Perhatikan gambar di bawah untuk memudahkan mencari nilai p dan q!
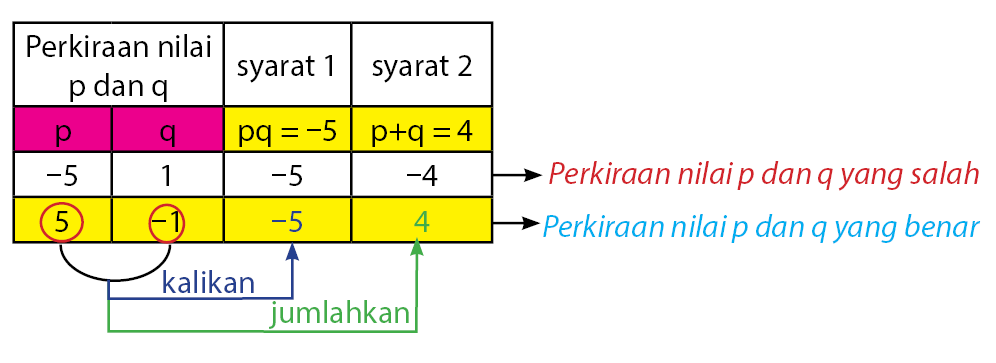
Sehingga diperoleh nilai p dan q yang memenuhi adalah p = 5 dan q = ‒1.
Hasil pemfaktoran: x2 + 4x ‒ 5 = (x + 5)(x ‒ 1)
bukan x2 + 4x ‒ 5 = (x ‒ 5)(x + 1).
Jadi, pernyatan yang benar adalah pernyataan I dan III.
Jawaban: C
Contoh 2 – Soal Pemfaktoran Bentuk Aljabar

Pembahasan:
Menyelidiki kebenaran dari setiap pemfaktoran yang diberikan pada soal.
Pernyataan (i): Benar
10x2 + 35x = 5x × 2x + 5x × 7
10x2 + 35x = 5x(2x + 7)
Pernyataan (ii): Salah
49x2 ‒ 36 = (7x)2 ‒ 62
49x2 ‒ 36 = (7x ‒ 6)(7x + 6)
Pernyataan (iii): Salah
(x ‒ 7)(x ‒ 4) = x(x ‒ 4) ‒ 7 (x ‒ 4)
= x2 ‒ 4x ‒ 7x + 28
= x2 ‒ 11x + 28
Pernyataan (iv): Benar
(3x + 5)(x ‒ 7) = 3x(x ‒ 7) + 5(x ‒ 7)
= 3x2 ‒ 21x + 5x ‒ 35
= 3x2 ‒ 16x ‒ 35
Jadi, pernyataan yang benar terdapat pada nomor (i) dan (iv).
Jawaban: B
Demikianlah tadi ulasan cara mengerjakan soal pemfaktoran bentuk Aljabar, mudah bukan? Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Menyelesaikan Persamaan Kuadrat dengan TRIK KUCING
Fransiska sae
fransiskasae@gmail.com
101005