Analisis regresi linear sederhana merupakan suatu cara untuk mendapatkan model prediksi melalui sebuah fungsi linear berdasarkan data-data yang ada. Teori dalam analisis regresi linear sederhana biasanya digunakan untuk mencari tahu hubungan antara dua variabel. Dua jenis variabel tersebut adalah variabel bebas atau variabel prediktor dan variabel terikat atau variabel respon. Variabel bebas biasanya disimbolkan X, sementara variabel terikat biasanya disimbolkan Y.
Bentuk hubungan dua variabel pada regresi linear sederhana umumnya terdiri atas 2 macam yaitu terdapat hubungan (positif atau negatif) dan tidak ada hubungan. Di mana deteksi awal bentuk hubungan antara dua variabel dapat dilihat melalui bentuk diagram pencar. Bila pencaran titik-titik data menunjukkan adanya suatu trend atau kecenderungan yang linear maka model regresi linier layak digunakan.

Jika diagram pencar dari data berada di sekitar suatu garis diagonal yang condong ke kanan maka menandakan data memiliki hubungan positif. Jika diagram pencar dari data berada di sekitar suatu garis diagonal yang condong ke kiri maka menandakan data memiliki hubungan negatif. Sementara jika diagram pencar data tidak membentuk suatu pola garis maka menandakan diagram tidak ada hubungan.
Diagram pencar yang membentuk suatu trend pola garis linear selanjutnya dapat dilakukan estimasi parameter model. Selain itu dalam analisis regresi juga mencakup uji signifikansi dan hipotesis untuk mengambil kesimpulan. Bagaimana cara membentuk persamaan analisis regresi linear sederhana? Bagaimana cara melakukan pengujian model persamaan regresi linear? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Rumus dan Bentuk Umum Persamaan Regresi Linear Sederhana
- Korelasi (r) dan Koefisien Determinasi (R2)
- ANOVA (Analysis of Variance) atau Uji F (Uji Serentak)
- Uji Hipotesis Parameter Regresi
- Pemeriksaan Asumsi Model Regresi Linear
Baca Juga: Contoh Soal Analisis Regresi Linear Sederhana dan Pembahasannya
Rumus dan Bentuk Umum Persamaan Regresi Linear Sederhana
Dalam analisis regresi linear sederhana perlu diperhatikan syarat kelayakannya. Beberapa syarat kelayakan yang harus dipenuhi dalam analisis regresi sederhana meliputi beberapa nomor berikut.
- Jumlah sampel yang digunakan memiliki jumlah sama
- Menggunakan satu variabel bebas
- Nilai residual berdistribusi normal
- Terdapat hubungan antara variabel bebas dan terikat
- Tidak terjadi gejala heteroskedastitas
- Tidak terjadi gejala autokorelasi untuk data time series (runtun waktu)
Syarat kelayakan model regresi linear sederhana dilakukan melalui beberapa uji seperti uji normalitas, uji linearitas, uji heteroskedastisitas, dan uji autokorelasi (untuk data time series).

Tujuan umum analisis regresi linear sederhana adalah untuk mengetahui pengaruh variabel bebas terhadap variabel terikat. Rumus regresi linear sederhana memenuhi bentuk persamaan umum: Y = β0 + β1X. Di mana Y adalah variabel terikat (dependent variable), X adalah variabel bebas (independent variable), serta β0 dan β1 adalah koefisien regresi.
Rumus yang digunakan untuk menentukan nilai β0 dan β1 sesuai dengan persamaan-persamaan berikut.
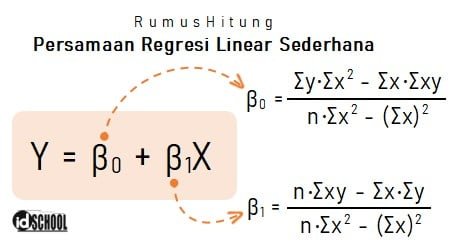
Nilai variabel terikat (Y) adalah nilai yang diprediksi, sedangkan besar peningkatan (+) atau penurunan (‒) ditunjukan melalui nilai koefisien regresi (b). Contoh cara mengartikan hasil persamaan, misalkan diperoleh persamaan regresi linear sederhana: Y = 46,2 ‒ 7,45X.
- Jika variabel bebas tidak memberikan pengaruh (X = 0) maka nilai variabel terikat Y = 46,2. Di mana nilai tersebut merupakan titik potong garis dengan sumbu vertikal (sumbu y).
- Untuk setiap kenaikan satu satuan nilai variabel bebas akan membuat nilai variabel terikat mengalami penurunan sebesar 7,45 satuan.
Baca Juga: Cara Eksplorasi Data dengan Statistik Deskriptif
Korelasi (r) dan Koefisien Determinasi (R2)
Kuat/tidaknya hubungan antara kedua variabel dalam model persamaan regresi linear diukur dengan koefisien korelasi (r). Di mana nilai r berada pada rentang ‒1 sampai dengan 1 (‒1 ≤ r ≤ 1).
Koefisien korelasi (r) yang semakin mendekati 1 menunjukkan hubungan positif semakin kuat antara kedua variabel. Sementara koefisien korelasi (r) yang semakin mendekati ‒1 menunjukkan hubungan negatif semakin kuat antara kedua variabel.
Hubungan antara variabel bebas dan terikat dapat berupa hubungan positif atau hubungan negatif.
- Hubungan positif: setiap kenaikan variabel bebas akan membuat variabel terikat juga mengalami kenaikan (nilai sebanding)
- Hubungan negatif: setiap kenaikan variabel bebas akan membuat variabel terikat mengalami penurunan (nilai berbanding terbalik)
Nilai korelasi dapat dihitung menggunakan rumus berikut:

Kuadrat dari korelasi (r) disebut dengan koefisien determinasi (KD atau R2) yang nilainya menunjukkan seberapa besar pengaruh variabel bebas terhadap variabel terikat.
Misalkan didapat nilai R2 = 0,5682 maka besar pengaruh variabel bebas terhadap varibel terikat adalah 56,82%. Sementara sisanya yaitu 100% ‒ 56,82% = 43,18% dijelaskan oleh peubah lain di luar persamaan. Hubungan pengaruh yang baik umumnya ditunjukkan melalui besar nilai R2 ≥ 60%.
ANOVA (Analysis of Variance) atau Uji F (Uji Serentak)
Model regresi dikatakan layak jika memiliki signifikansi pada ANOVA yang dapat diketahui melalui nilai p value atau F hitung pada tabel ANOVA. Tabel ANOVA yang digunakan untuk menentukan F hitung memiliki bentuk seperti berikut.
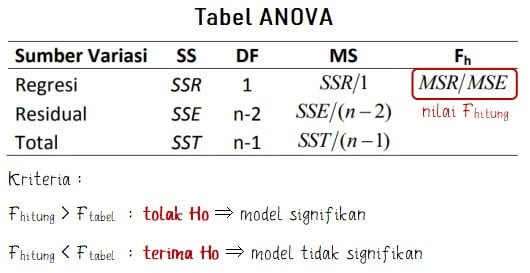
Di mana SSR, SSE, dan SST secara urut merupakan jumlah kuadrat regresi, jumlah kuadrat residual/ erros, dan jumlah kuadrat total. Ketiga nilai tersebut merupakan properti of Least Square fit yang memiliki bentuk rumus seperti persamaan-persamaan berikut.

Nilai p (p-value) merupakan ukuran probabilitas kekuatan dari bukti untuk menolak atau menerima hipotesis yang diajukan (H0). Model regresi yang signifikan ditandai dengan nilai p value kurang dari α (0,05). Semakin kecil nilai p yang diperoleh maka semakin kuat bukti tersebut untuk menolak hipotesis null.
Dalam aplikasinya kita biasanya membandingkan dengan nilai alpha yang digunakan. Jika p-value kurang dari α maka tolak H0 (model signifikan), sedangkan jika p-value lebih dari α maka gagal tolak H0 (model tidak signifikan).
Baca Juga: Perbedaan Penelitian Kualitatif dan Kuantitatif
Uji Hipotesis Parameter Regresi
Hipotesis adalah asumsi atau pernyataan yang mungkin benar atau mungkin salah mengenai suatu populasi. Hipotesis yang akan diuji dinyaktakan dengan H0 (hipotesis nol), sedangkan lawan dari hipotesis uji adalah H1.
- Hipotesis:
H0: β1 = 0
H1: β1 ≠ 0
Pengujian hipotesis dilakukan untuk mengambil keputusan apakah suatu hipotesis yang diajukan diterima atau ditolak. Penolakan H0 memiliki makna penerimaan hipotesis lainnya yaitu H1.
Kritria penolokan hipotesis null (H0):
- |thitung| > t½α, n‒2
- p-value < α
- Selang kepercayaan untuk β1 tidak memuat nol
Pemeriksaan Asumsi Model Regresi Linear
Regresi linear sederhana menggunakan asumsi agar taksiran parameter dalam model bersifat BLUE (Best, Linear, Unbiased, dan Estimator). Di mana analisis regresi linear sederhana menggunakan beberapa asumsi yang perlu diperiksa dan diuji. Beberapa asumsi yang perlu diperhatikan dalam analisis regresi linear sederhana meliputi linearitas, kebebasan ragam, kehomogenan ragam, dan kenormalan.
1) Asumsi Linearitas
Uji linearitas digunakan untuk mengetahui apakah variabel-variabel penelitian mempunyai hubungan yang linear. Vara melakukan uji linearitas dalam analisis regresi linear sederhana dapat dilakukan dengan scatter ploth graph atau compare means.
Untuk pengujian dengan scatter plot dapat dilakukan dengan melihat pola kecenderungan atau trend dari plot-plot (titik-titik) data. Jika diagram plot menunjukkan kecenderungan garis lurus maka dapat disimpulkan bahwa data memiliki sifat linear. Jika diagram plot tidak mmembentuk kecenderungan garis lurus maka tidak terdapat sifat linear (memiliki sifat non linear).
Sementara untuk pengujian melalui compare means dapat dilakukan dengan melihat signifikansi pada tabel ANOVA. Jika nilai signifikansi kurang dari 0,05 maka memenuhi sifat linearitas.
2) Asumsi Kebebasan Ragam (Independensi)
Pengujian asumsi kebebasan ragam berkaitan erat dengan masalah autokorelasi. Tolak ukur ada atau tidaknya masalah autokorelasi dilakukan melalui uji Durbin-Watson (DW) dengan ketentian sebagai berikut.
- DW < ‒2: terjadi autokorelasi positif
- ‒2 < DW < +2: tidak terjadi autokorelasi
Asumsi kebebasan ragam akan otomatis terpenuhi untuk data yang diperoleh dari responend acak (random) dengan teknik probability sampling.
3) Asumsi Kehomogenan Ragam (Uji Heteroskedastisitas)
Heteroskedastisitas adalah kondisi di mana terdapat perbedaan variansi residual dari satu pengamatan ke pengamatan lainnya. Lawannya adalah homogenitas yaitu kondisi di mana terdapat kesamaan variansi residual dari satu pengamatan ke pengamatan lainnya.
Uji heteroskedastitas bertujuan untuk mengetahui apakah dalam model regresi terjadi ketidaksamaan variansi residual dari satu pengamatan ke pengamatan lain. Model regresi yang baik terdapat pada data yang tidak mengalami hetroskedastisitas.
- Hipotesis:
H0 = ragam galat homogen (tidak terdapat kasus heteroskedastisitas)
H1 = ragam galat tidak homogen (terdapat kasus heteroskedastisitas)
Pengujian heteroskedastisitas dapat menggunakan beberapa metode seperti uji Glejser, uji Park, atau uji koefisien korelasi Spearman.
Gejala heteroskedastisitas dalam model regresi secara umum ditandai melalui nilai p-value atau signifikansi (sign.) kurang dari 0,05. Atau dapat dikatakan bahwa model regresi yang baik ditandai dari nilai signifikansi hasil uji lebih dari 0,05.
4) Asumsi Kenormalan (Normalitas)
Uji normalitas dalam analisis regresi linear sederhana bertujuan menguji apakah dalam model regresi memiliki residual yang berdistribusi normal. Jika asumsi ini dilanggar maka uji statistik akan menjadi tidak valid (bias), terutama untuk sample kecil. Uji normalitas dapat dilakukan dengan dua pendekatan yaitu grafik dan nilai signifikansi (p-value).
Pendekatan dengan grafik dilakukan dengan melihat histogram dan P‒P plot. Untuk data menyebar merata di sekitar garis lurus pada pendekatan grafik normal menunjukkan terpenuhinya asumsi kenormalan.
Sementara untuk nilai signifikansi dapat dilakukan dengan menganalisis nilai p-value pada uji Koglmogorov-Smirnov, Chi-Square, Liliefors, atau Saphiro-Wilk. Di mana nilai signifikansi lebih besar dari 0,05 (α = tingkat kepercayaan 95%) menunjukkan data berdistribusi normal. Sementara nilai signifikansi lebih kecil dari 0,05 menunjukkan data tidak berdistribusi normal.
- Hipotesis:
H0 = ragam galat berdistribusi normal (Sign. > 0,05)
H1 = ragam galat tidak berdistribusi normal (Sign. < 0,05)
Demikianlah tadi ulasan bagaimana proses dasar untuk melakukan analisis regresi linear sederhana. Di mana analisis regresi mencakup pembuatan model dan pengujian model tersebut. Terima kasih sudah mengungjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Langkah Kerja yang Perlu Dilakukan dalam Metode Penelitian Kuantitatif