Analisis regresi linear adalah suatu model yang dapat digunakan untuk melakukan prediksi atau peramalan. Dalam regresi terdapat cara untuk mecari tahu bagaimana hubungan variabel-variabel yang digunakan dalam suatu penelitian. Regresi dalam KKBI memiliki makna penyusutan luas yang disebabkan faktor tertentu. Dalam statistika, regresi dipahami sebagai metode analisis untuk meilihat pengaruh suatu faktor (variabel bebas) terhadap variabel terikat (nilai yang menjadi prediksi).
Variabel yang digunakan pada analisis regresi terdiri daru dua jenis yaitu variabel bebas (independent variabel) dan variabel terikat (dependent variabel). Variabel bebas disebut juga variabel penjelas atau variebal eksplanatorik adalah jenis variabel yang memengaruhi. Variabel terikat adalah jenis variabel yang dipengaruhi. Simbol untuk variabel bebas biasanya meggunakan huruf X, sementara simbol untuk variabel terikat biasanya menggunakan huruf Y.
Analisis regresi linear terdiri dari dua jenis yaitu regresi linear sederhana dan regresi linear berganda. Dua jenis analisis regresi tersebut memiliki bentuk persamaan linear yang berbeda. Di mana persmaan regresi sederhana memuat satu variabel terikat dan satu variabel bebas. Sementara persamaan regresi linear berganda memuat satu variabel terikat dan beberapa variabel bebas.
Bagaimana cara menyatakan hubungan antar variabel dalam analisis regresi? Bagaimana persamaan regresi sederhana? Bagaimana bentuk persamaan regeresi linear berganda? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Baca Juga: Statistik Deskriptif dan Infernesial, Apa Bedanya?
Analisis Regresi Linear Sederhana
Analisis regresi linear sederhana digunakan untuk mengetahui pengaruh variabel bebas terhadap variabel terikat. Rumus regresi linear sederhana memenuhi bentuk persamaan umum: Y = a + bX. Di mana Y adalah variabel terikat (dependent variable), X adalah variabel bebas (independent variable), a adalah konstanta, dan b adalah koefisien regresi.

Nilai variabel terikat (Y) adalah nilai yang diprediksi, sedangkan besar peningkatan atau penurunan ditunjukan melalui nilai koefisien regresi (b). Hubungan antara variabel bebas dan terikat dapat berupa hubungan positif atau hubungan negatif.
- Hubungan positif terdapat pada variabel terikat dan variabel bebas yang memiliki hubungan sebanding. Di mana setiap kenaikan variabel bebas akan membuat variabel terikat juga mengalami kenaikan.
- Hubungan negatif terdapat pada variabel terikat dan variabel bebas yang memiliki hubungan berbanding terbalik. Di mana setiap kenaikan variabel bebas akan membuat variabel terikat mengalami penurunan.
Cara mendapatkan persamaan regresi linear sederhana sesuai dengan data yang dimiliki dapat dilakukan dengan dua cara. Cara pertama dengan melalukan perhitungan manual, sedangkan cara kedua dengan alat bantu analisis statistik seperti SPSS, R, atau Minitab.
Baca Juga: Contoh Analisis Regresi Linear Sederhana
Analisis Regresi Linear Berganda
Analisis regresi linear berganda adalah model regresi digunakan pada penelitian dengan jumlah variabel bebas lebih dari satu. Regresi linear berganda dapat menunjukkan bagaimana hubungan antara dua atau lebih variabel bebas (x1, x2, …) dengan variabel terikat (Y).
Persamaan regresi linear berganda memiliki bentuk umum: Y = a + b1x1 + b2x2 + … + bnxn. Di mana Y adalah variabel terikat; x1, x2, … xn adalah variabel bebas, a adalah konstanta, dan b adlaag koefisien regresi.

Nilai variabel terikat (Y) adalah nilai yang diprediksi, sedangkan besar peningkatan atau penurunan dinyatakan melalui nilai koefisien regresi (b). Hubungan antar variabel dalam regresi linear sederhana juga dapat berupa hubungahn positif dan hubungan negatif.
Cara mengetahui hubungan positif dan hubungan negatif pada regresi linear berganda dilakukan dengan mengamati bentuk persamaan. Untuk koefisien regresi yang memiliki tanda positif menunjukkan tedapat hubungan positif antara variabel bebas dengan variabel terikat. Untuk koefisien regresi yang memiliki tanda negatif menunjukkan tedapat hubungan negatif antara variabel bebas dengan variabel terikat.
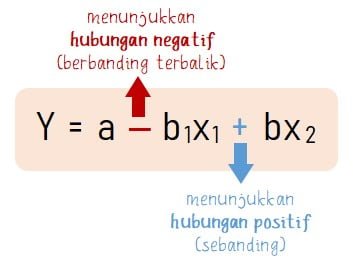
Misalnya, suatu data memiliki hubungan regresi linear berganda dengan persamaan Y = 40,5 ‒ 7,5x1 + 10,2x2. Dari persamaan yang diperoleh dapat diketahui bahwa koefisien regresi variabel bebas pertama (x1) bertanda negatif yaitu b1 = ‒7,5. Sedangkan koefisien regresi variabel bebas kedua (x2) bertanda positif yaitu b2 = 10,2. Sehingga dapat disimpulkan bahwa,
- Variabel bebas pertama (x1) memiliki hubungan negatif dengan variabel terikat (Y), kerena koefisien regresi b1 bernilai negatif (b1 = ‒7,5).
- Variabel bebas kedua (x2) memiliki hubungan negatif dengan variabel terikat (Y), kerena koefisien regresi b2 bernilai positif (b2 = 10,2).
Sama seperti regresi sederhana, persamaan regresi linear berganda dari suatu data dapat ditentukan melalui dua cara. Cara pertama dengan melalukan perhitungan manual dan cara kedua dengan alat bantu analisis statistik seperti SPSS, R, atau Minitab.
Demikianlah tadi ulasan regresi linear sederhana dan berganda yang meliputi bentuk persamaan dan apa perbedaan keduanya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Baca Juga: Contoh Analisis Regresi Linear Berganda
Terima kasih bang, materinya sangat mudah dipahami dan terperinci sekali.