Tabel distribusi frekuensi adalah salah satu bentuk penyajian data kelompok. Salah satu cara membuat tabel distrubusi frekuensi adalah aturan Aturan Sturges. Aturan berlaku untuk menentukan banyak kelas dan panjang kelas.
Bentuk peyajian data dalam tabel distribusi frekuensi lebih ringkas dan menarik. Sehingga perlu untuk dipelajari. Tabel distribusi frekuensi terdiri dari tabel distribusi frekuensi tunggal dan kelompok. Dua bentuk tabel distribusi frekuensi ada di bawah.

Bagaimana cara membuat tabel distribusi frekuensi ada di bawah.
Daftar isi:
Baca Juga: Cara Membuat Ogive Positif dan Negatif
Rumus Aturan Sturgess
Aturan Struges berguna untuk menyajikan data dalam kelas-kelas yang memiliki interval sama. Caranya menggunakan rumus k = 1 + 3,3 log n.
- Keterangan:
- k = jumlah kelas
- n = banyaknya data
Rumus Aturan Struges untuk menentukan banyak kelas:

Untuk panjang kelas dapat menggunakan rumus jangkauan dibagi k. Jangkauan adalah salah satu ukuran penyebaran data. Nilanya sama dengan selisih nilai terendah dengan nilai tertinggi. Jangkauan = xmaks – xmin.
Sehingga, rumus panjang kelas adalah:
Contoh penyajian data dalam bentuk tabel distribusi frekuensi.

Keterangan:
- Kelas: sebuah kelompok interval nilai
- Batas kelas: nilai terendah (batas bawah kelas) dan tertinggi (batas atas kelas)
- Tepi bawah kelas:
Tb = batas bawah kelas ‒ 0,5 - Tepi atas kelas:
Tb = batas bawah kelas + 0,5 - Panjang kelas (ℓ): banyak data dalam satu interval kelas, ℓ = Ta ‒ Tb
- Nilai tengah: xi = ½ × (batas kelas bawah + batas kelas atas)
Baca Juga: Rumus Ragam (Variansi) untuk Sampel dan Populasi
Cara Membuat Tabel Distribusi Frekuensi
Langkah-langkah membuat tabel distribusi frekuensi kelompok:
- Mengurutkan data
- Menentukan banyak kelas
- Menentukan panjang kelas
- Menghitung banyak frekuensi setiap kelas, gunakan turus
- Menyajikan tabel distribusi frekuensi
Bagaimana caranya ada di bawah.
Soal:
Berikut adalah data tinggi badan sejumlah siswa.
| 164 | 154 | 148 | 145 | 180 |
| 175 | 172 | 160 | 152 | 155 |
| 153 | 158 | 162 | 165 | 167 |
| 165 | 161 | 157 | 170 | 166 |
| 150 | 153 | 158 | 160 | 162 |
| 178 | 174 | 165 | 167 | 170 |
| 155 | 172 | 155 | 164 | 165 |
| 158 | 160 | 167 | 158 | 161 |
1) Mengurutkan data
Langkah pertama adalah mengurutkan data yang akan disajikan. Dari langkah ini akan bergunak untuk mendapatkan nilai terbesar dan terkecil. Selain itu juga berguna untuk menentukan frekuensi data dari setiap kelas.
Data yang telah diurutkan.
| 145 | 148 | 150 | 152 | 153 |
| 153 | 154 | 155 | 155 | 155 |
| 157 | 158 | 158 | 158 | 158 |
| 160 | 160 | 160 | 161 | 161 |
| 162 | 162 | 164 | 164 | 165 |
| 165 | 165 | 165 | 166 | 167 |
| 167 | 167 | 170 | 170 | 172 |
| 172 | 174 | 175 | 178 | 180 |
2) Menentukan banyak kelas tabel distribusi frekuensi
Selanjunya adalah menentukan banyak kelas dengan Aturan Sturges. Rumus yang digunakan adalah k = 1 + 3,3 ⋅ log n (diketahui nilai log 40 = 1,602).
Banyak kelas:
k = 1 + 3,3×log 40 = 1 + 3,3×1,602
k = 1 + 4,806 = 5,806 ≈ 6
3) Menentukan panjang kelas
Langkah berikutnya adalah menentukan panjang kelas. Rumus panjang kelas adalah ℓ = jangkauan/k = xmax – xmin/k . Dari data diketahui xmax = 180, xmin = 145, dan k = 6.
Sehingga,
4) Menentukan frekuensi setiap kelas
Beriktunya adalah menentukan kelas-kelas intervalnya.
Dari perhitungan diperoleh panjang kelas adalah ℓ = 6. Batas bawah kelas pertama sama dengan data terkecil. Sedangkan batas atas kelas pertama adalah data terkecil + (panjang kelas ‒ 1).
Data yang akan disajikan memiliki nilai terkecil = 145 sehingga,
- kelas pertama memiliki
- batas bawah = 145
- batas atas = 145 + (6 ‒ 1) = 145 + 5 = 150
Untuk interval kelas berikutnya mengikuti cara di atas. Sampai diperoleh enam kelas dengan intreval 145 ‒ 150; 151 ‒ 156; 157 ‒ 162; 163 ‒ 168; 169 ‒ 174; dan 175 ‒ 180.
Frekuensi setiap kelas dicari menggunakan turus seperti cara berikut.
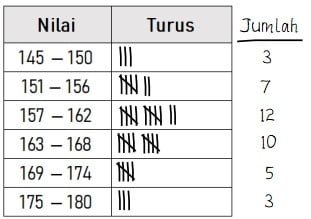
5) Penjian tabel distribusi frekuensi
Selesai! Dapat disajikan data seperti berikut.
| Kelas | Frekuensi |
| 145 ‒ 150 | 3 |
| 151 ‒ 156 | 7 |
| 157 ‒ 162 | 12 |
| 163 ‒ 168 | 10 |
| 169 ‒ 174 | 5 |
| 175 ‒ 180 | 3 |
Baca Juga: Rumus Mean Median Modus untuk Data Kelompok
Kelemahan Aturan Sturgess
Aturan Sturgess memiliki kelemahan untuk data dengan jangkayan yang lebar. Kondisi ini membuat beberapa data dengan nilai yang besar tidak masuk dalam tabel distribusi frekuensi.
Contoh kelemahan penyajian tabel distribusi frekuensi terdapat pada data berikut.
| 164 | 154 | 148 | 145 | 181 |
| 175 | 172 | 160 | 152 | 155 |
| 153 | 158 | 162 | 165 | 167 |
| 165 | 161 | 157 | 170 | 166 |
| 150 | 153 | 158 | 160 | 162 |
| 178 | 174 | 165 | 167 | 170 |
| 155 | 172 | 155 | 164 | 165 |
| 158 | 160 | 167 | 158 | 161 |
Data terurut yang sesuai dengan himpunan data di atas:
| 145 | 148 | 150 | 152 | 153 |
| 153 | 154 | 155 | 155 | 155 |
| 157 | 158 | 158 | 158 | 158 |
| 160 | 160 | 160 | 161 | 161 |
| 162 | 162 | 164 | 164 | 165 |
| 165 | 165 | 165 | 166 | 167 |
| 167 | 167 | 170 | 170 | 172 |
| 172 | 174 | 175 | 178 | 181 |
Dari data dapat diperoleh nilai-nilai berikut.
- Jumlah data: n = 40
- Panjang kelas:
k = 1 + 3,3 log 40 = 1 + 3,3 × 1,602
k = 5,806 = 6 (bulat ke atas)
- Nilai terkecil: xmin = 145
- Nilai terbesar: xmaks = 181
- Jangkauan:
J = 181 ‒ 145
J = 36
- Panjang kelas:
ℓ = 36 : 6
l = 6
Diperoleh tabel distribusi frekuensi kelompok seperti contoh sebelumnya. Namun pada data ini, terdapat nilai 181 (data terbesar) yang tidak masuk dalam tabel.
Penyebaran data yang sesuai untuk data baru ditunjukkan seperti tabel berikut.

Baca Juga: Cara Membaca Diagram Kotak Garis (Boxplot)
Itulah salah satu contoh kelemahan aturan Sturgess. Untuk mengatasi data seperti di atas dapat menggunakan aturan lain.
Sekian ulasan cara membuat tabel distribusi frekuensi berdasar Aturan Sturgess. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

trus itu kalau 1 datum gamasuk solusinya apa? apa ud biarin aja gtu? tar klo mau cari mean median modusnya 1 datum itu ga dimasukkin?
Bisa dicoba metode lain untuk menentukan panjang kelas dalam distribusi frekuensi, misalnya Metode Scott
Kemarin jg menemui banyak kelas tidak sama dengan perhitungan.
Ketika dihitung dengan rumus = 6 kelas
Saat ditabelkan ada 7.
Jadi bagaimana