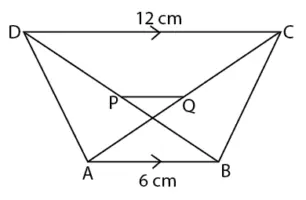
P dan Q adalah titik tengah diagonal trapesium ABCD

Pembahasan:

Ada dua cara yang dapat digunakan untuk menghitung panjang PQ. Cara pertama menggunakan langkah runut dengan rumus kesebangunan pada trapesium. Cara kedua dengan rumus cepat yang diperoleh dari penurunan persamaan kesebangunan.

Bagaimana kedua cara pengerjaan akan ditunjukkan melalui dua pembahasan di bawah.

Cara 1: Langkah Runut

Misalkan titik R adalah titik perpotongan antara ruas garis PQ dan garis BC. Pertama, perhatikan segitiga ABC dan BCD dalam trapesium ABCD. Dari kesebangunan segitiga CQR dan segitiga CAB didapat persamaan QR : AB = CQ : CA.

Selanjutnya perhatikan segitiga BPR dan BCD dalam trapesium ABCD. Kesebangunan pada segitiga BPR dan segitiga BCD menghasilkan persamaan PR : DC = BP : BD.

Dari persamaan dari kesebangunan pada segitiga-segitiga dalam trapesium ABCD akan menghasilkan persamaan-persamaan berikut.

• Persamaan (i):
  ^QR/_AB = ^CQ/_CA 
  QR = ^AB×CQ/_CA 

• Persamaan (ii):
  ^PR/_DC = ^BP/_BD
  PR = ^DC×BP/_BD 

Berdasarkan karakteristik trapesium sama kaki, panjang diagonal trapesium sama kaki adalah kongruen. Sehingga dapat diperoleh persamaan panjang BD = AC. Diketahui diketahui P dan Q adalah titik tengah diagonal trapesium ABCD, maka panjang BP = BD = AQ = QC.

Dengan demikian, bentuk persamaan (i) dapat dirubah menjadi bentuk persamaan (i): QR = ^AB×BP/_BD. Sedangkan bentuk persamaan (ii) tetap menjadi persamaan (ii): PR = ^DC×BP/_BD.

Panjang garis PQ = PR ‒ QR, di mana persamaan untuk PR = persamaan (i) dan QR = persamaan (ii). Substitusi persamaan (i) dan (ii) pada persamaan PQ = PR ‒ QR.

PQ = PR ‒ QR
PQ = ^DC×BP/_BD ‒ ^AB×CQ/_BD
PQ = ^{DC×BP ‒ AB×BP}/_BD
PQ = ^{BP(DC ‒ AB)}/_BD

Dari informasi yang diberikan pada soal dapat diketahui bahwa panjang DC = 12 cm, AB = 6 cm, dan BD = 2BP. Substitusi nilai-nilai tersebut pada persamaan PQ = ^{BP(DC ‒ AB)}/_BD akan menghasilkan nilai panjang PQ.

PQ = ^{BP(12 ‒ 6)}/_2BP
PQ = ^{12 ‒ 6}/₂
PQ = ⁶/₂ = 3 cm

Jadi, jika diketahui P dan Q adalah titik tengah diagonal trapesium ABCD maka panjang PQ = 3 cm.

Cara 2: Cara Cepat

Penyelesaian yang kedua akan dilakukan dengan rumus cepat untuk menghitung PQ jika diketahui P dan Q adalah titik tengah diagonal trapesium ABCD. Cara menghitung panjang PQ dengan rumus cepat dilakukan dengan cara berikut.

PQ = ½× selisih panjang sisi sejajar trapesium

Diketahui bahwa trapesium ABCD memiliki sisi sejajar DC = 12 cm dan AB = 6 cm. Sehingga panjang PQ dapat dicari tahu dengan cara berikut.

PQ = ½ × (DC ‒ AB)
PQ = ½ × (12 ‒ 6)
PQ = ½ × 6 = 3 cm

Jadi, jika diketahui P dan Q adalah titik tengah diagonal trapesium ABCD maka panjang PQ adalah 3 cm.

Jawaban: C